Venn Diagram Examples for Problem Solving
Sometimes the problems cannot be solved as easily as we want them to be, so for making it easier to understand them in order to simplify the tasks, it is better to create a diagram. In this way, with the help of a drawing, it can become clear what to focus on as well as what aspects to pay more attention to.
Having the examples of the problem-solving process in a way of a Venn diagram may lead to making it possible to create the needed scheme of what should be done as well as what work should be finished first within some project or an organization as a whole.
Any Venn diagram can also be called as a primary one. The other names for it are logic diagram, set diagram, etc. It is simply one of the so many types of the diagrams that are used for showing all the possible logical relations between some finite collection of a few or a lot of the different sets.
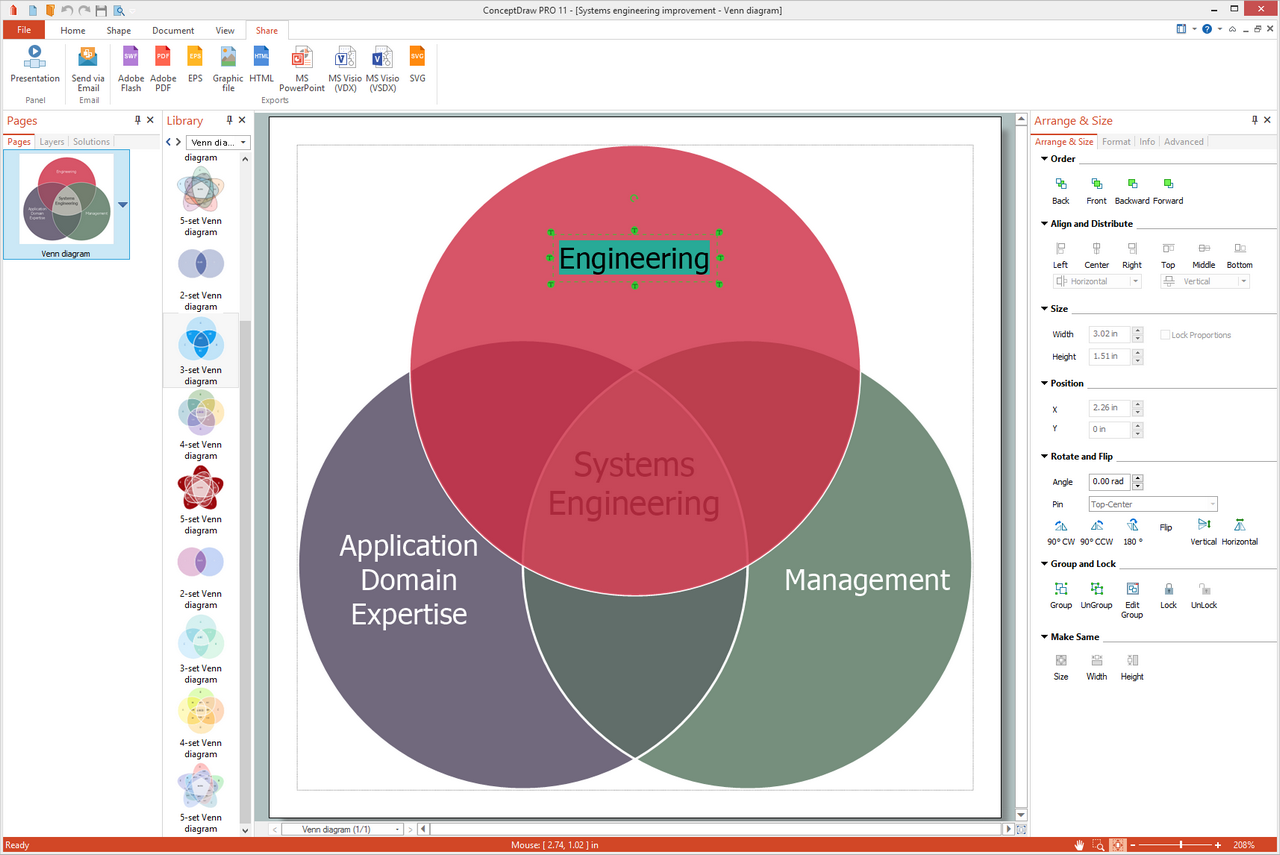
Example 1. Venn Diagram Problem Solving
The mentioned type of diagrams can be also used for depicting different elements in a way of the points in the plane as well as the sets in a way of the regions that can be found inside some closed curves. Any Venn diagram created with the help of the ConceptDraw DIAGRAM software may consist a lot of the overlapping closed curves such as circles, each of which is known for representing some set.
The mentioned points inside each of the curves are labelled with a letter “S” representing the elements of the set S in this way. At the same time, the points that can be found outside the boundary, are those which represent the elements which cannot be found in the “S” set.
In this way, the set of all the existing elements (which are known to be members of both sets S and T) can be represented in a visual way by the area of the overlap of the “T” and “S” regions.
In Venn diagrams the curves are usually overlapped in the way its creator wants them to be, showing all the possible relations in between the previously described sets. The mentioned “Venn diagrams” were conceived by John Venn in about 1880.
Since then, they are used for teaching the so-called “elementary set theory”. Besides, they can be also used for illustrating some simple set relationships in either logic, statistics, probability, linguistics or computer science, or both.
Any Venn diagram in which the area of each of its shapes seems to be proportional to the number of all the elements that it contains, is known to be called as a “scaled” or an “area-proportional” Venn diagram that is being constructed with the simple closed curves drawn in a plane.
The principle of all the Venn diagrams is that the sets (also known as “classes”) can be represented by regions in a special relation to one another. Due to such relation, all the possible logical relations of the mentioned classes can be indicated in the very same diagram showing the connections to each other.
In this way, the diagram leaves enough room for any possible relation of the classes to illustrate, and the given (or “actual”) relation can be after specified by indicating that some region is either not-null or null.
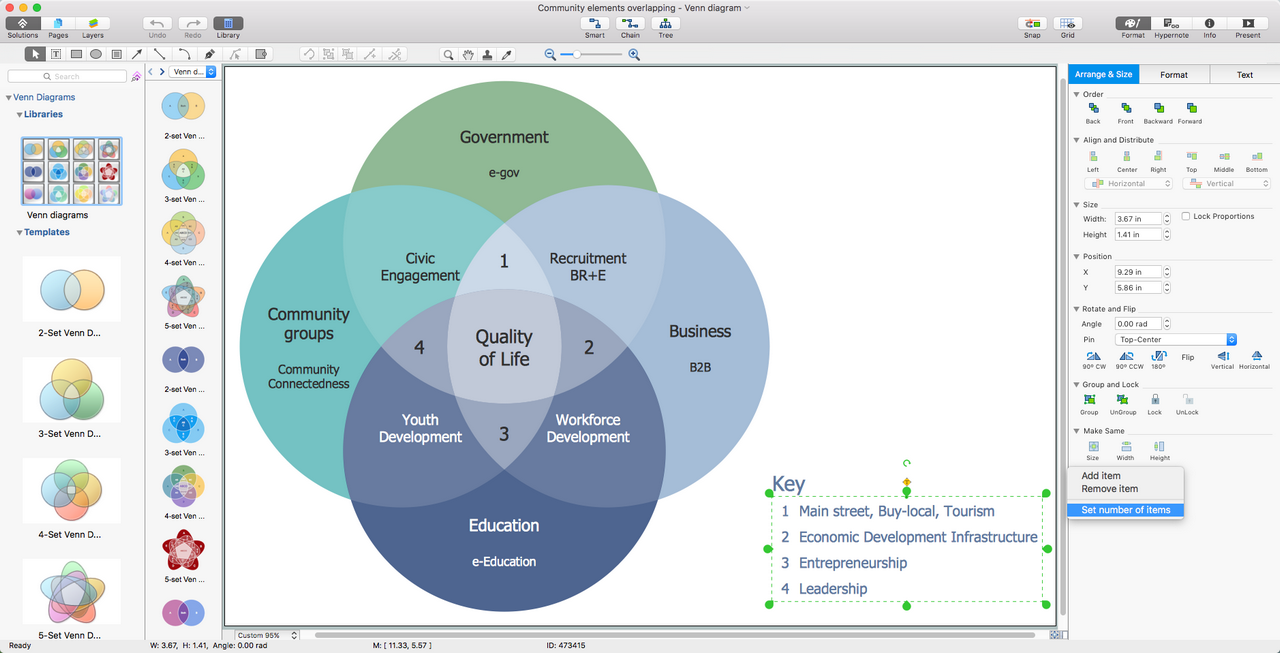
Example 2. Venn Diagram Problem Solving
Venn diagrams usually are those that comprise the overlapping circles and the interior of such circles can symbolically represent all the elements that the set includes. At the same time, the exterior is known to be representing those elements that are not members of the set and so they are not connected with it at all.
After being introduced by John Venn in 1880, the Venn diagrams were further developed in the 20th century. Thus, in 1963 D. W. Henderson showed that the existence of an n-Venn diagram that has n-fold rotational symmetry implied that n was a key number, called as “prime”. It was also showed that all symmetric Venn diagrams exist when n is either 7 or 5.
Venn diagrams are known to be similar to Euler diagrams, but still the first ones are more commonly used and many of those who made them know, that each of such diagrams for n component sets has to contain all 2n possible zones that are known to be corresponding to some combination of either exclusion or inclusion in each of the existing component sets.
It is also widely known that, to compare to the Venn diagrams, the Euler ones contain only the actually possible zones in some given context, but both Euler diagrams as well as Venn diagrams were incorporated as part of instruction in a so-called “set theory” in the 1960s as part of the new math movement. Since then, they have also been adopted in the curriculum of many other fields and nowadays they can be used for most of the needed problem-solving processes as long as there is enough information to add to them.
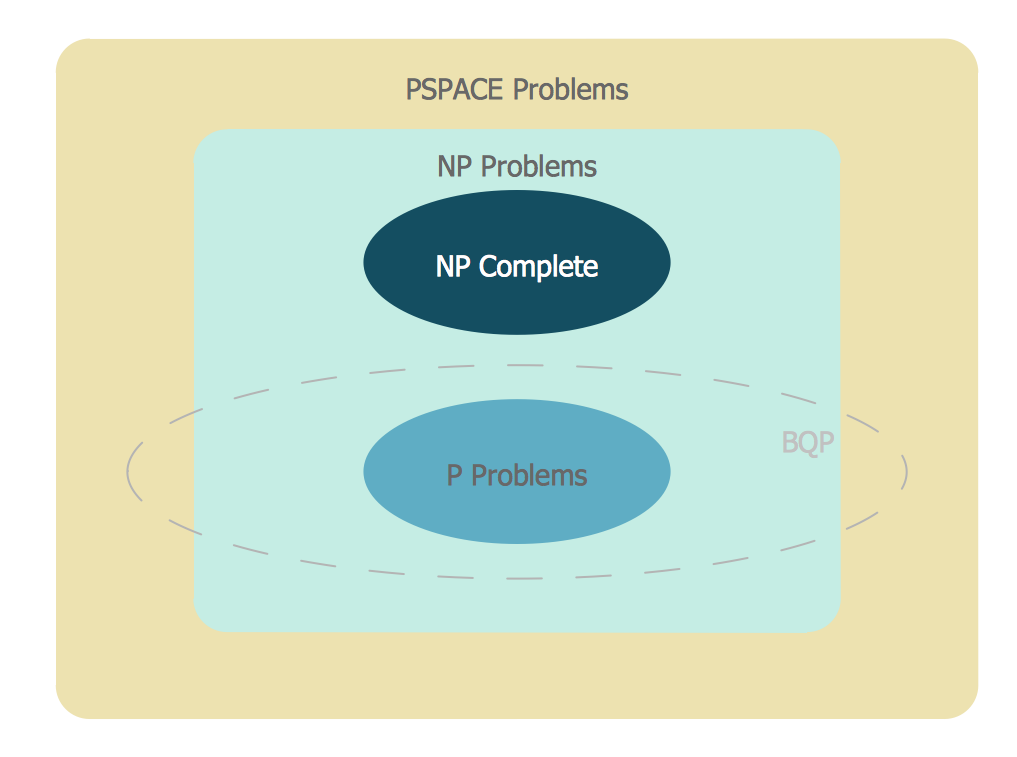
Example 3. Venn Diagram Problem Solving — BQP Complexity. The suspected relationship of BQP to other problem spaces.
In the Business Diagrams solution, there are the pre-made examples that can be always used for making the unique, great looking diagrams, such as the 2-set Venn ones of any needed colour, the 3-set one, the 4-set ones and the 5-set ones. Having the already previously created samples of the Venn diagrams can help any ConceptDraw DIAGRAM user make it possible to make the needed drawing within only a few minutes by editing the existing ones.
Taking this opportunity of using the already previously design diagrams, such as the Venn ones from the Business Diagrams solution, can simplify your work of the drawings and save your time. One of the examples, that is available for all the ConceptDraw DIAGRAM users is the “Venn Diagram — Internet Marketing Professions”. Next, the “Venn Diagram — Path to Sustainable Development” is another template of the Venn diagram created by using three circles where such notes as “Environmental”, “Social” and “Economic” are used.
TEN RELATED HOW TO's:
Process mapping helps with sharing business results and reorganizing workflow. In almost every case, after creating a sales process flowchart the steps that are redundant become obvious for a manager. It's easy to find a flowchart examples that will help in developing one for your business.
This sales process flowchart consists of a sequence of steps that represent a simple sale process. Each step is shown graphically by a rectangle representing processing steps or an activity, or a diamond representing a decision. These rectangles are linked by arrows, that indicate the direction of the sales workflow. ConceptDraw Sales Flowcharts solution delivers a the full set of classical flowchart notation symbols, along with sales-related icons and pictograms.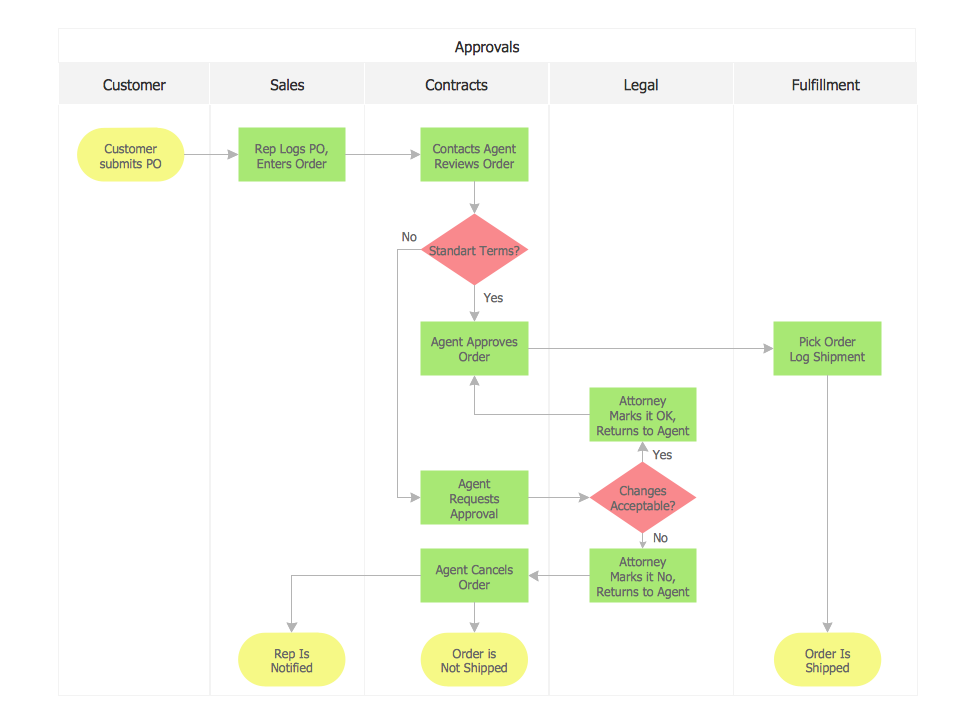
Picture:
Sales Process Flowchart
Flowchart Examples
Related Solutions:
Communication via Internet nowadays is almost irreplaceable part of lifestyle. It’s needless to say that providing that communication is not a piece of cake, and network diagram software is useful for representing all the interconnections between network devices. These diagrams are also helpful for educational purposes.
This drawing depicts the network topology of the sample web studio. This is a physical type of network diagram. It is depicting the network, end-user equipment and connections between them. The given network has combined the both star and mesh network topology features. This diagram is a tool of network administrator. it delivers the actual information on location of servers, hubs, switches, routers, and other telecommunication equipment. The collection of network related symbols provided with ConceptDraw Network Diagrams solution represents the entire network components. All Symbols are standard. Therefore, network specialists can effortlessly decrypt this diagram.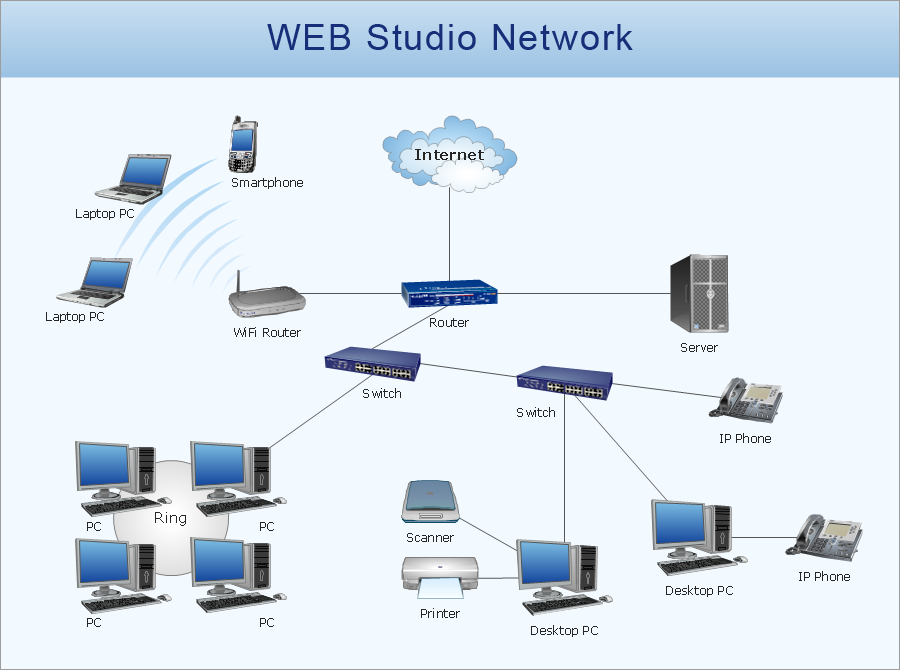
Picture: Network Diagram Software
Related Solution:
Event-Driven Process chain Diagrams for improvement throughout an organisation. Best software for Process Flow Diagram. The Event-driven Process Chain (EPC) Diagrams allows managers to plan processes and resources.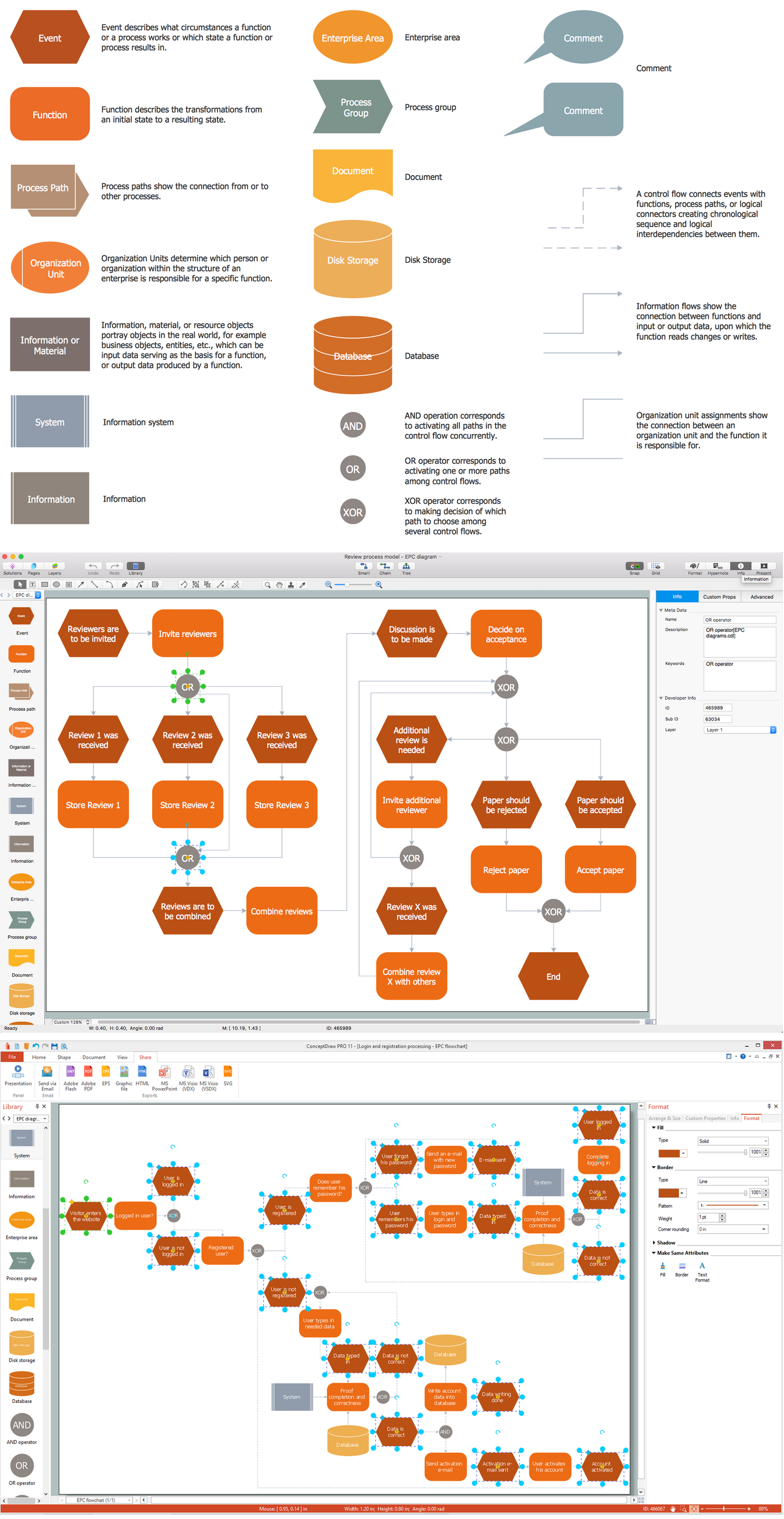
Picture: Business process Flow Chart — Event-Driven Process chain (EPC) diagrams
Related Solution:
The Ishikawa diagram, Cause and Effect diagram, Fishbone diagram — all they are the names of one and the same visual method for working with causal connections. Originally invented by Kaoru Ishikawa to control the process quality, the Ishikawa diagram is well proven in other fields of management and personal scheduling, events planning, time management. It is a chart in the form of a fish, whose head is a problem, the fins are variants for its causes.
To design easily the Fishbone diagram, you can use a special ConceptDraw DIAGRAM vector graphic and diagramming software which contains the powerful tools for Fishbone diagram problem solving offered by Fishbone Diagrams solution for the Management area of ConceptDraw Solution Park.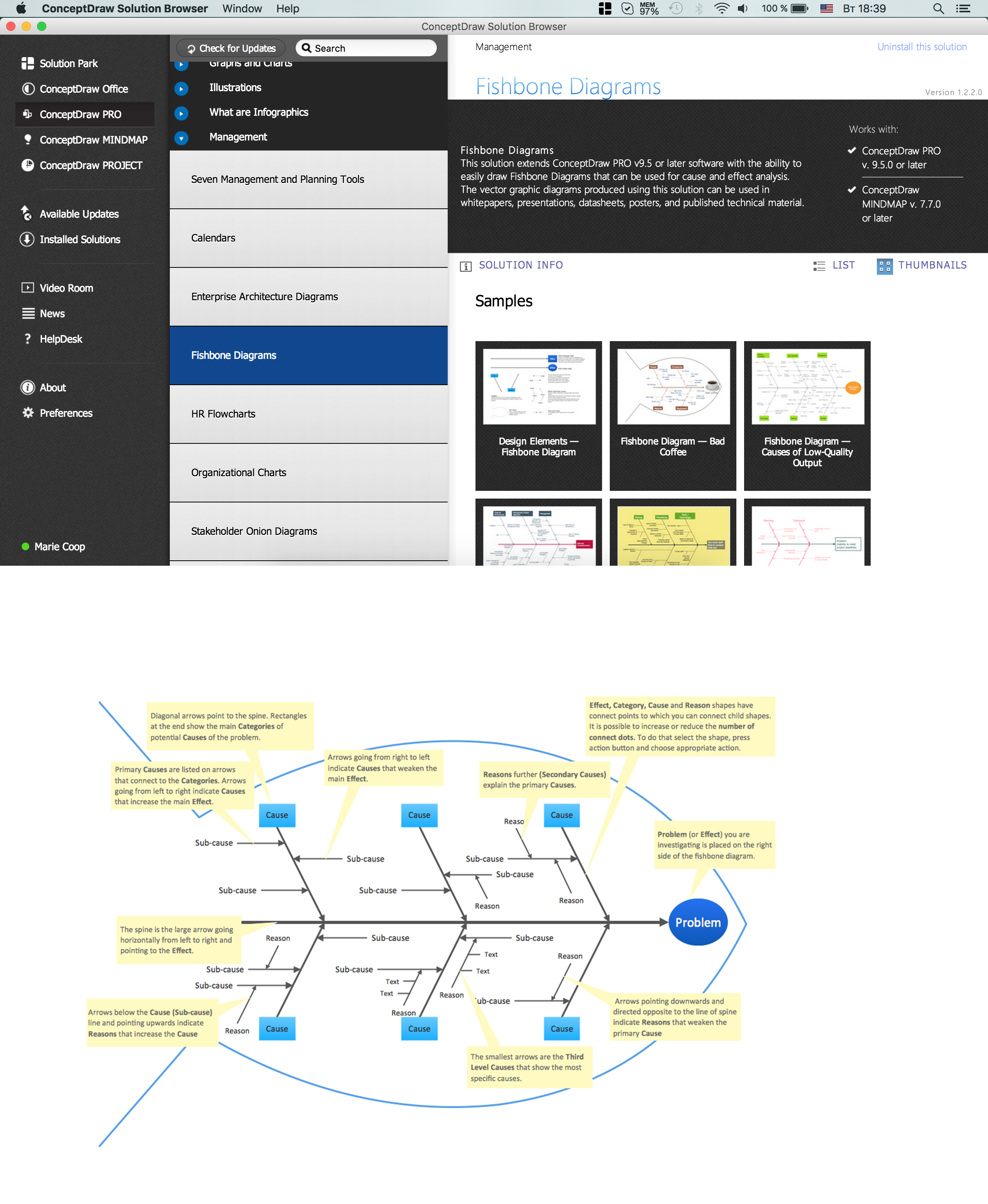
Picture: Fishbone Diagram Problem Solving
Related Solution:
Relationships Analysis. Relations Diagram - factors analysis, factors relations. Create Relations Diagram with ConceptDraw DIAGRAM.
The Seven Management and Planning Tools is a tool for Interaction diagram drawing. This diagram identifies causal relationships. Determine what factors are causes and which factors are effects. Interaction diagram helps establish KPIs to monitor changes and the effectiveness of corrective actions in resolving the problem.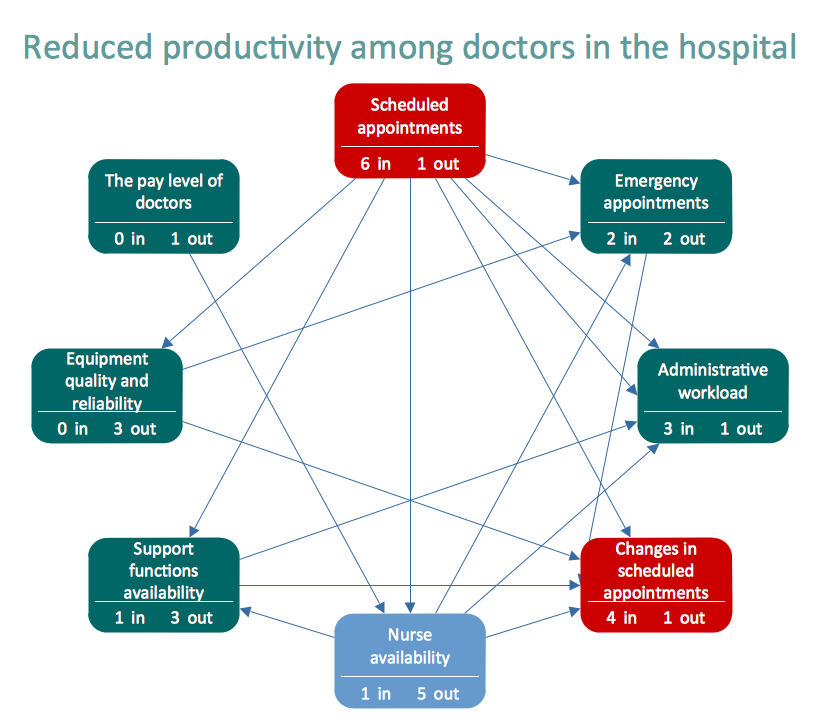
Picture: Relationships Analysis
Structured-systems analysis and design method uses data flow diagrams to represent the process of data flowing through a system. Talking about this might be useless without a proper example of DFD for online store (Data Flow Diagram). This DFD example shows all the distinctness that a diagram can bring into a scattered data structure.
Data flow diagrams are used to show how data is processed within some business processes. Making DFD is a common practice for business process modeling and analysis. This diagram represents the online store business flow. It describes inputs and outputs within online selling process and depicts the interactions between its participants. This DF diagram can be used by system analysts to create an overview of a business, to study and discover its inherent strengths and weak points.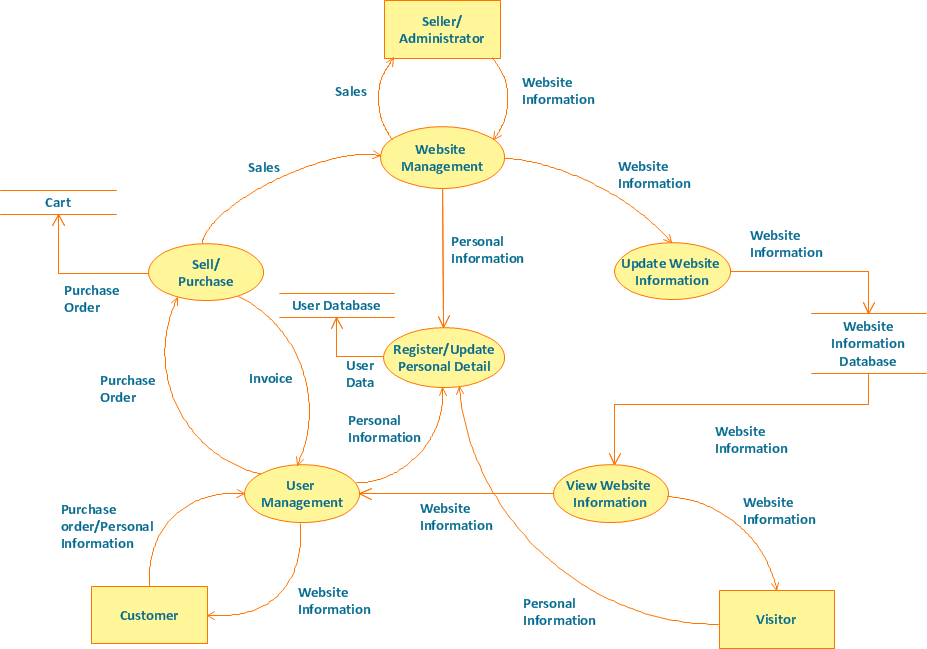
Picture: Example of DFD for Online Store (Data Flow Diagram)
Related Solution:
The activity of any organization is more or less branchy network of processes. The description of these processes is a hard technical task which requires definite methodology and standards.
According to the IDEF0 standard any process can be described in the form of a block (Activity Box) which has inputs and outputs. The process consists in transformation of inputs into outputs under the influence of the management and in the presence of necessary resources. Outputs of the given process later on can be either inputs for the next process or resources, or management means.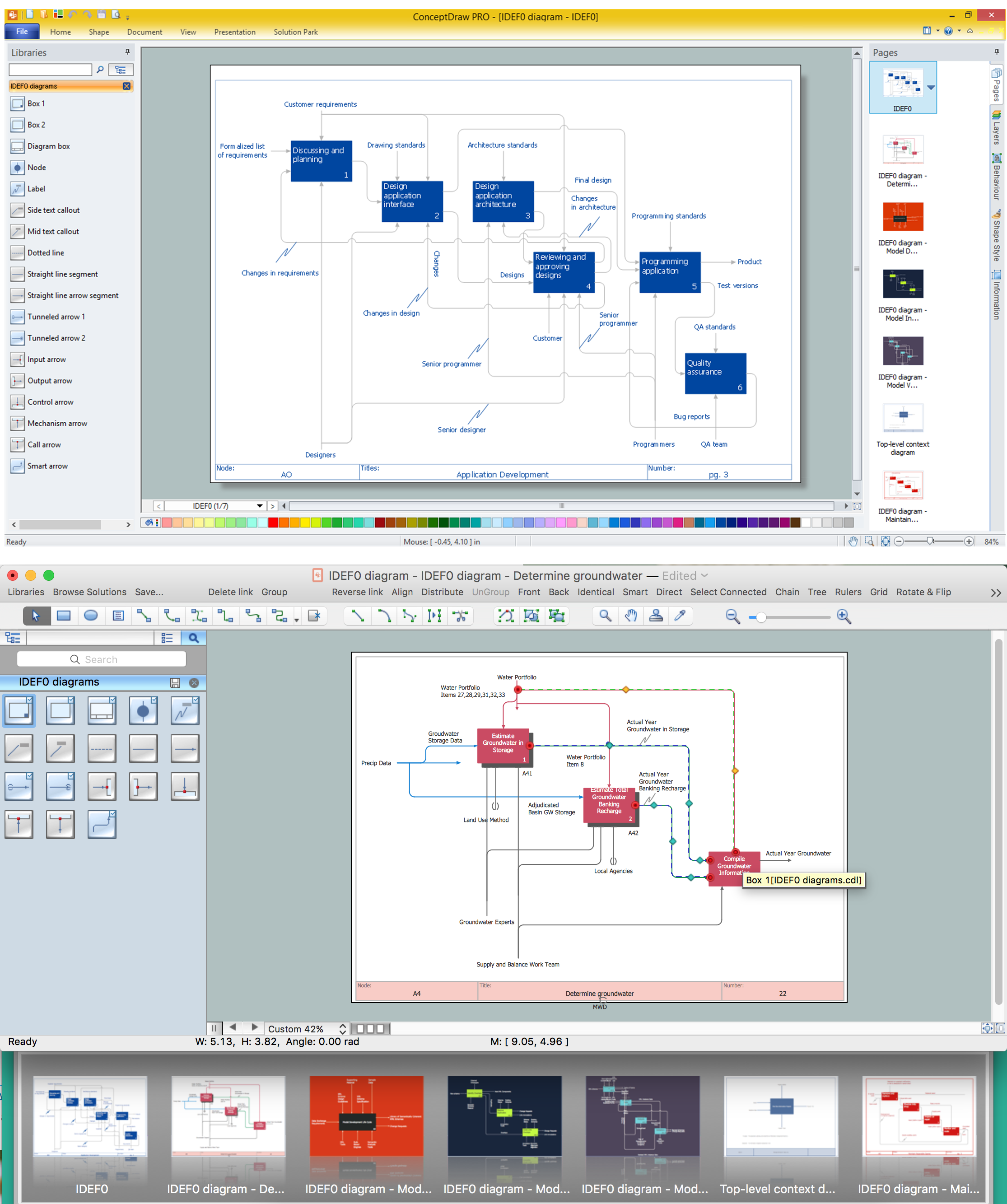
Picture: IDEF0 standard with ConceptDraw DIAGRAM
Related Solution:
This sample was created in ConceptDraw DIAGRAM diagramming and vector drawing software using the UML Class Diagram library of the Rapid UML Solution from the Software Development area of ConceptDraw Solution Park.
This sample describes the use of the classes, the generalization associations between them, the multiplicity of associations and constraints. Provided UML diagram is one of the examples set that are part of Rapid UML solution.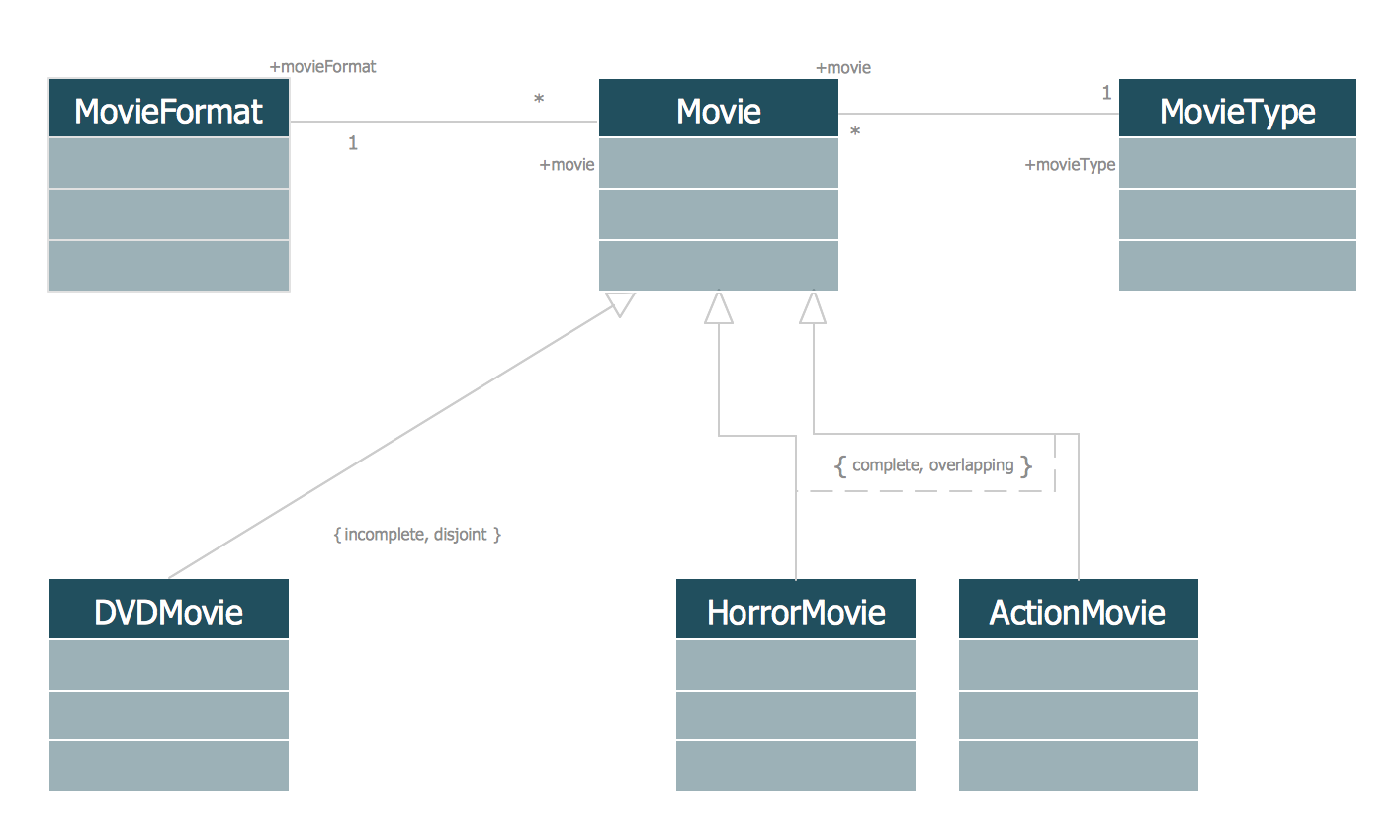
Picture: UML Class Diagram Generalization ExampleUML Diagrams
Related Solution:
The visual form of mind maps is helpful in all stages of quality management, from describing problem to describing and documenting a decision.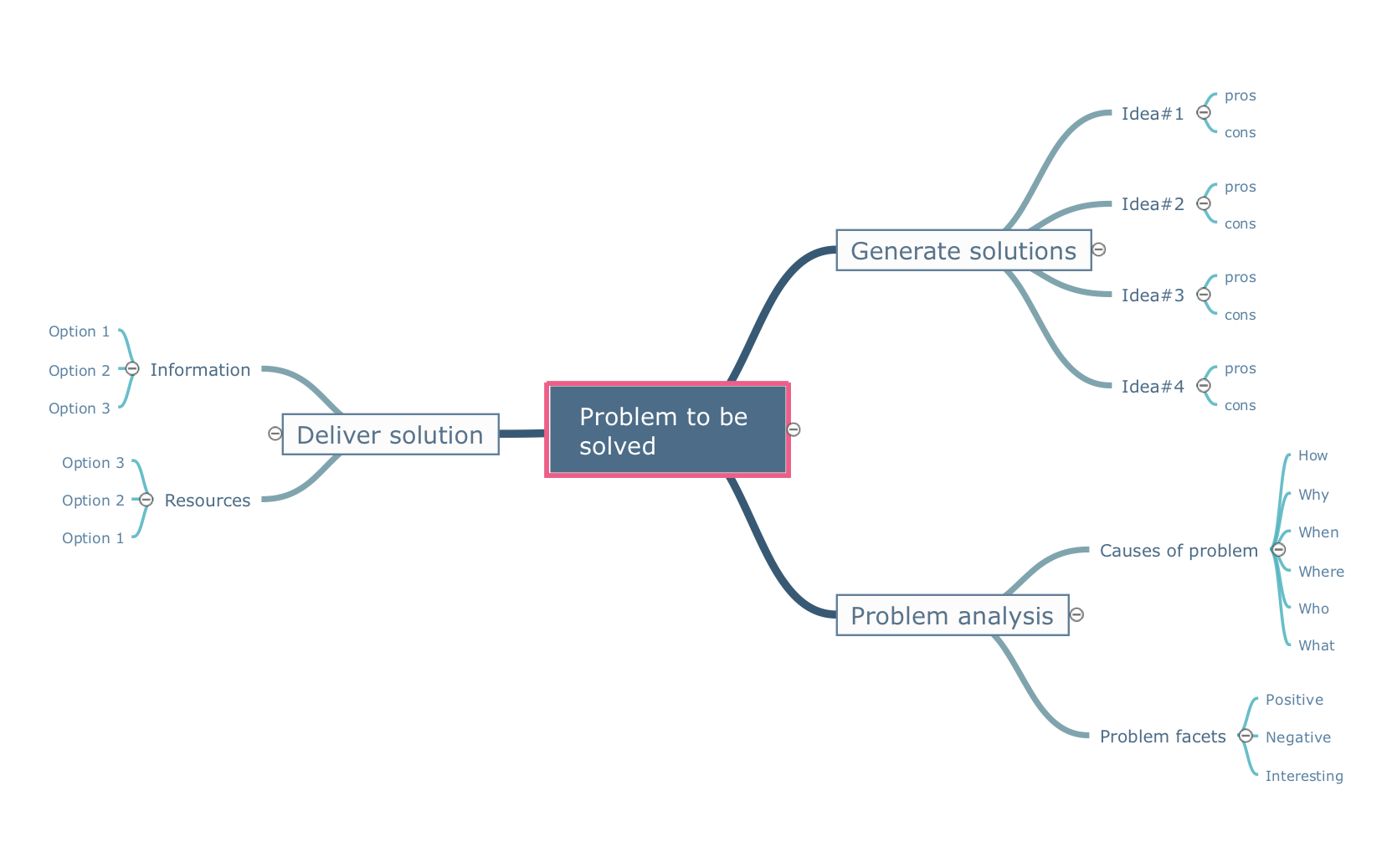
Picture: Quality Project Management with Mind Maps
Related Solution:
As restaurant industry is growing rapidly nowadays, researches show that almost half of the adults have worked in a restaurant or a cafe. Moreover, many of them dream to start their own someday. Unfortunately, it takes a lot of time to write a business plan and to find a great location, although some know how to create a restaurant floor plan in minutes or how to plan budget effortlessly. Hiring employees can also cause a lot of headache, but this is crucial for further success, because every guest comes to restaurant for a good service and delicious food. It is also worth noting that restaurant concept is also important, because it defines target audience and influences the menu.
This diagram represents the floor plan of an ongoing sports-theme establishment - restaurant, cafe, or other food service. A number of widescreen monitors installed along the perimeter provide visitors the opportunity to follow the course of a match from anywhere in the dining room of restaurant or cafe. The most of sports fans believe that food and alcohol is a big part of any sports show. That is why the dining room takes the most space - almost 60% of the total establishment space. Nearly all sports fans consume beverages while watching sports - beer, soda or water at least. Thus, the restaurant floor plan designers added a large lavatory there. Moreover, project developers considered unnecessary the gender division of such delicate place - perhaps they guess that only men are watching football, or believe that alcohol will eliminate the most of gender differences.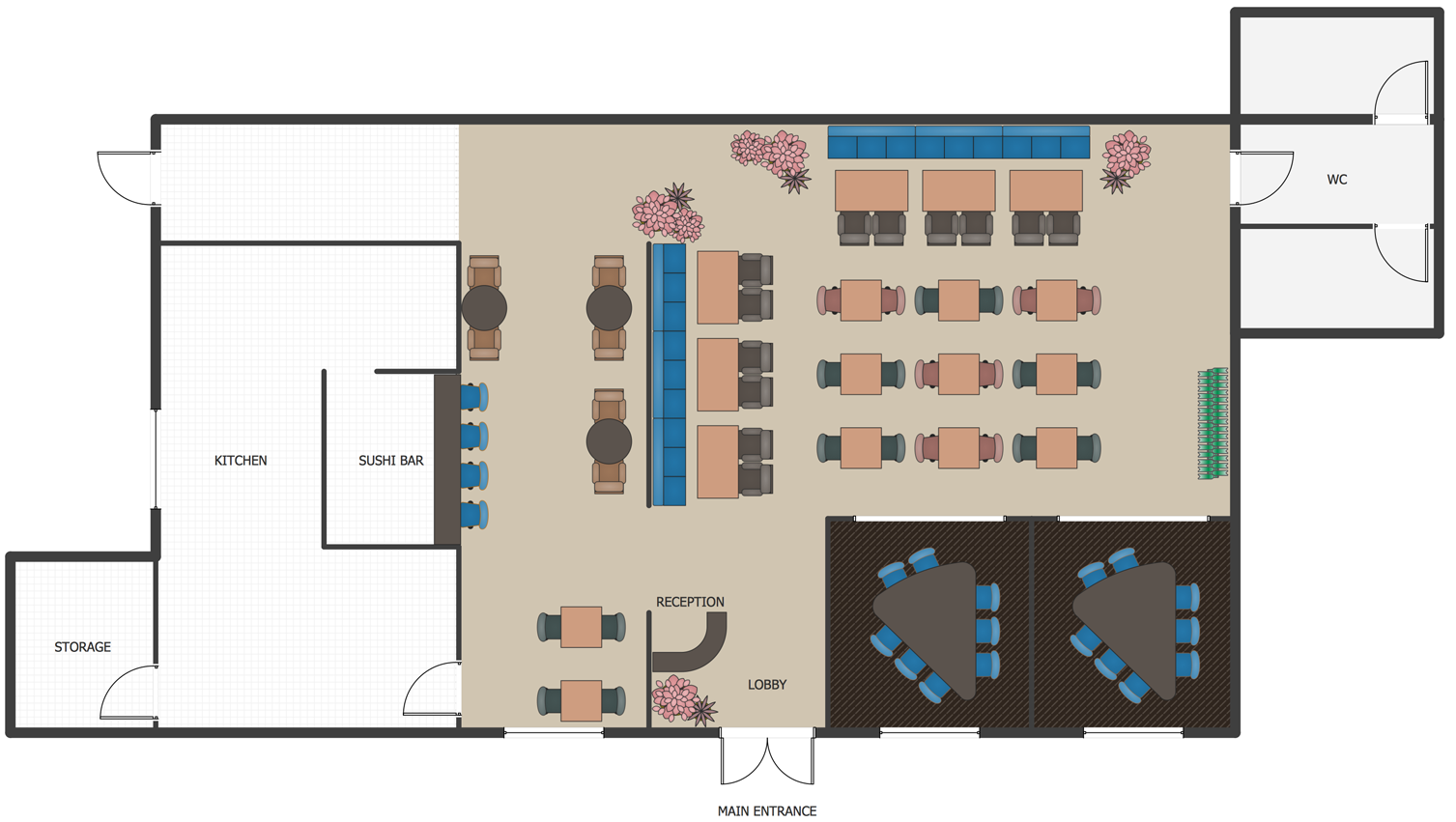
Picture: How To Create Restaurant Floor Plan in Minutes
Related Solution: