FSM — Finite-state Machine

A “finite-state machine” is also known to be called “finite automaton”, “finite-state automaton” or simply a “state machine”, being a “mathematical model of computation”. Being an abstract machine in exactly one of a finite number of states at some given time. The finite-state machine is known for being able to change from being in one particular state to another, doing it in response to some external inputs. Such change from one state to another is known to be called a “transition”. Any finite-state machine can be defined by its initial state, a list of its states and the conditions for each of the existing transitions.

The behaviour of any of the state machines can be checked by using many different devices in order to perform a pre-determined sequence of different actions, which may depend on a sequence of different events which they are presented with. The examples of the finite-state machine may be the vending machines, dispensing products once the proper combination of the coins is deposited. The elevators may be also a very good example of the finite-state machine, or FSM. The sequence of stops all the elevators make can be determined by the quantity of the floors requested by its riders. The traffic lights may be another example of the finite-state machines changing their sequence every time the cars have to wait stopping. All the combination locks require the input of the combination of the different numbers in some definite, proper order, that’s why they are a good example of the FSM as well.

The finite state machine is known to be having less computational power comparing to some other models of computation, for example, the so called “Turing machine”. The mentioned “computational power distinction” may mean there are the computational tasks that each Turing machine can do, but which a FSM one can not. The reason for this is a FSM's memory being quite limited by the number of the states which it has. The finite-state machines are known to be studied in the more general field of the so called “automata theory”. The complete action's information is never described in the table, but it can only be added by using the so called “footnotes”. A FSM definition is always possible by using the so called “state tables”.

The Unified Modelling Language has a notation for describing state machines. UML state machines are known to be introducing the new concepts of the so called “hierarchically nested states” as well as “orthogonal regions” during the process of extending the so called “notion of actions”. UML state machines have the characteristics of both “Mealy machines” and so called “Moore machines”, known to be supporting the actions depending on the triggering event as well as on the state of the system, as well as entry and exit actions, which are associated with states rather than transitions.

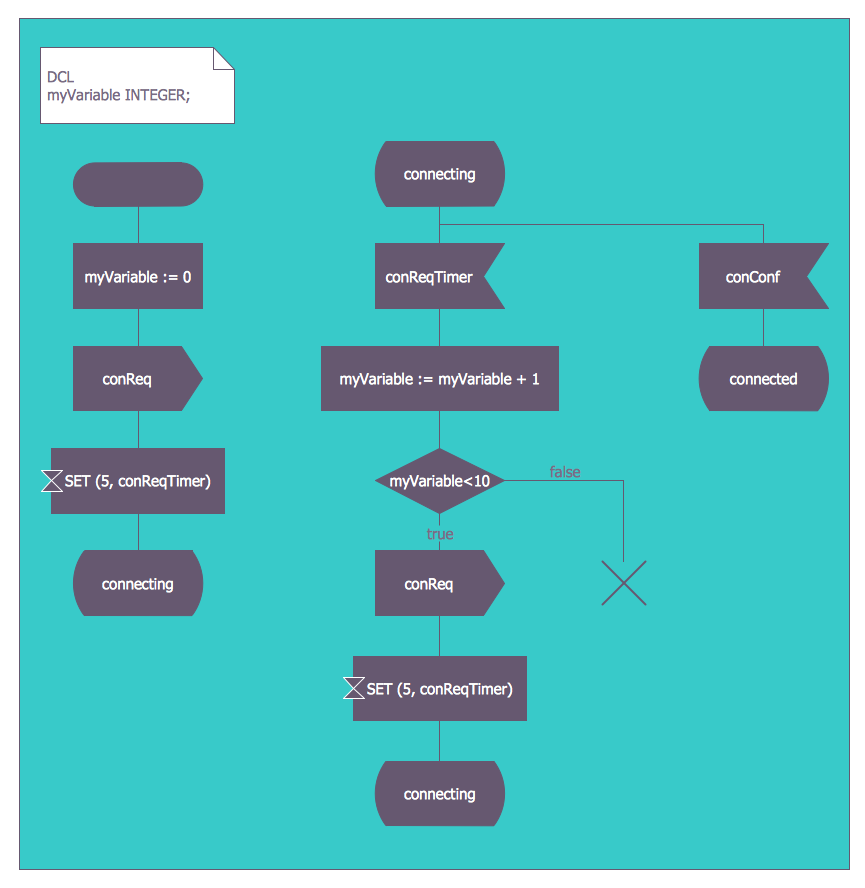
The Specification and Description Language is a standard from ITU. It includes numerous graphical symbols for describing different actions in the transition – for example, to send an event, to start a timer, to cancel a timer, to receive an event, to start another state machine, etc. There are many different variants used for representing a FSM, knowing to be significant in many different areas, including electrical engineering, computer science, mathematics, philosophy, biology, logic, linguistics, etc. One of the classes of the automata studied in the so called “automata theory” as well as the “theory of computation” is a finite state machine, widely used in computer science for modeling the application behaviour, for designing different hardware digital systems, as well as used in software engineering, network protocols, the study of computation, languages and compilers.

It is possible to subdivide the finite state machines into acceptors, classifiers, transducers and sequencers. The acceptors are also known to be called as “recognizers and sequence detectors”, producing the binary output and indicating if received input is accepted or not. Each of the possible states of any FSM is either "not accepting" or "accepting". As long as all input is received, in case its current state is an accepting one, then the input is known to be “accepted”. And vice versa, in case its current state is a rejecting one, then it is known to be “rejected”. As a general rule, any input is a sequence of symbols and actions are not normally used.

A set of the mentioned symbol sequences is known to be called as a “regular language”, but only in case there is some finite state machine that accepts exactly that set. For example, the set of binary strings with an even number of zeroes is a regular language, while the set of all strings which length is a prime number is not a regular language. A machine can be described as the one containing a string, which is accepted by the mentioned machine, but not the rejected ones. Thus, that language is known to be "accepted" by the machine, called the “regular languages”. Any language is known to be called as “regular” in case there is some finite-state machine accepting it. An instance of the algebraic path problem is determining the language which was accepted by a so called “finite state acceptor”. It is itself simply a generalization of the shortest path problem to graphs with edges which are weighted by the elements of a semi-ring.

To create FMS diagram, all you need is ConceptDraw DIAGRAM diagramming and drawing software. It is always better, though, to have a Specification and Description Language (SDL) Solution from ConceptDraw STORE application to simplify your work with drawing any FMS related drawings any complexity as the mentioned solution offers the pre-made examples as well as the stencil libraries with the design elements that all can be used while working in ConceptDraw DIAGRAM

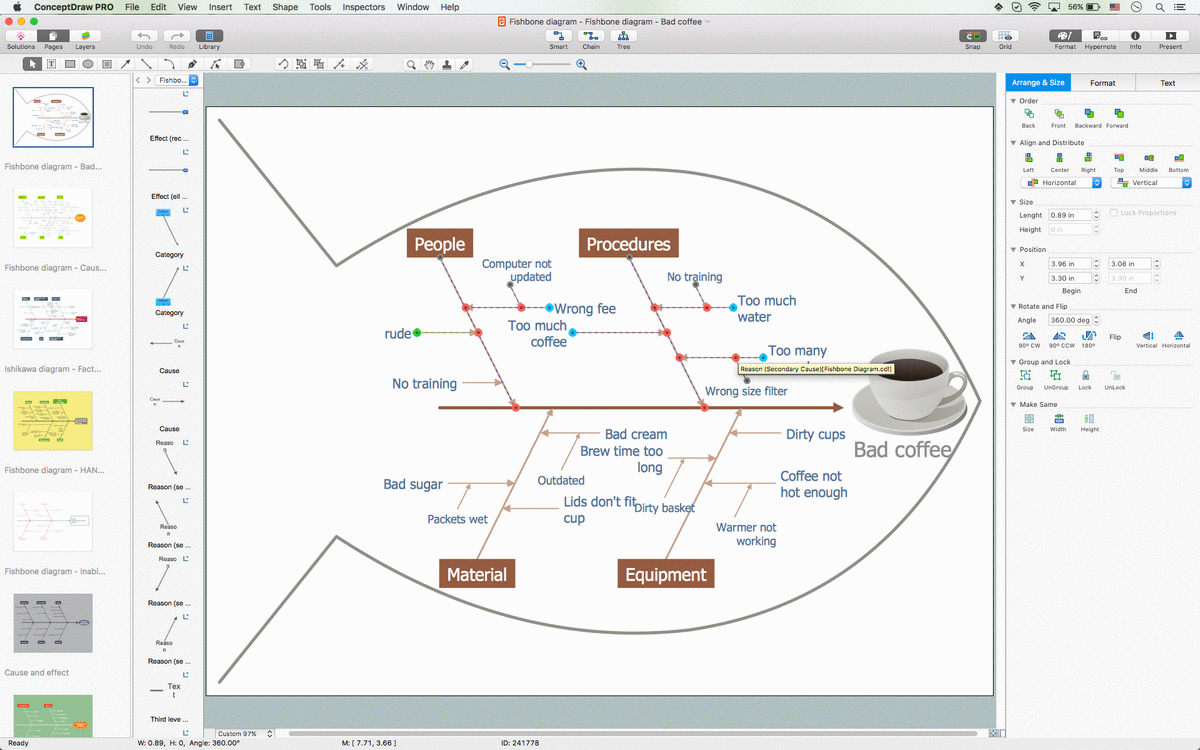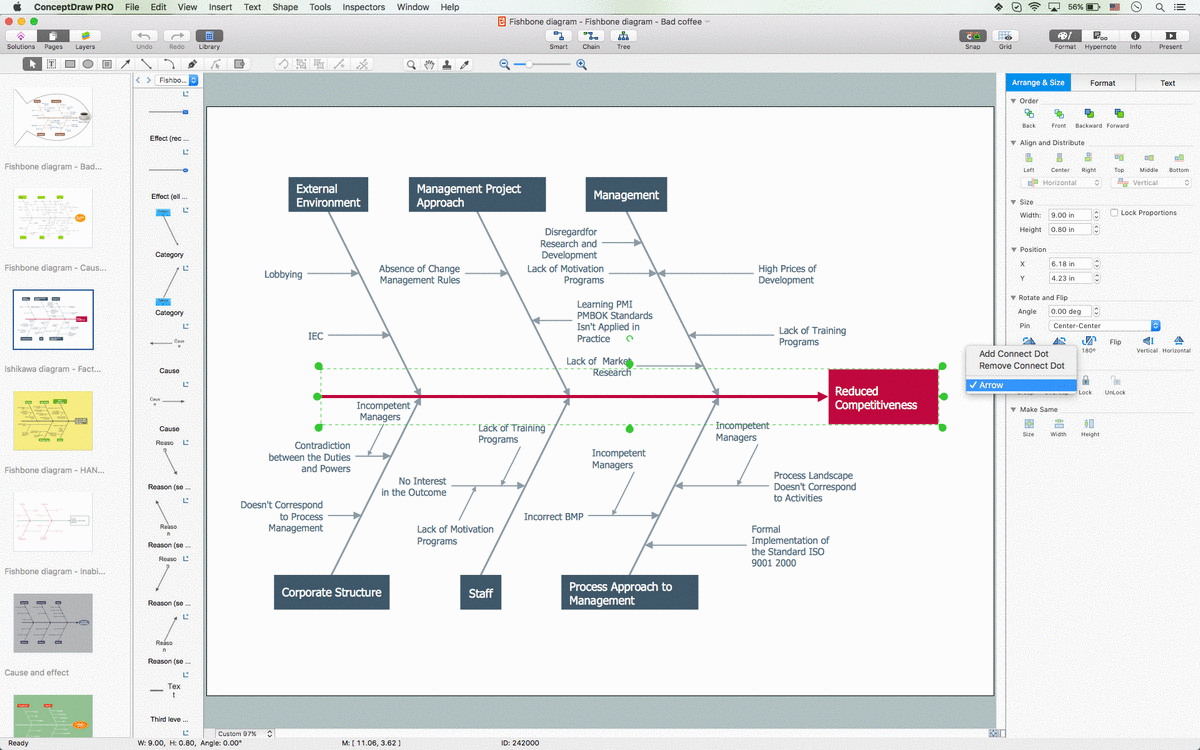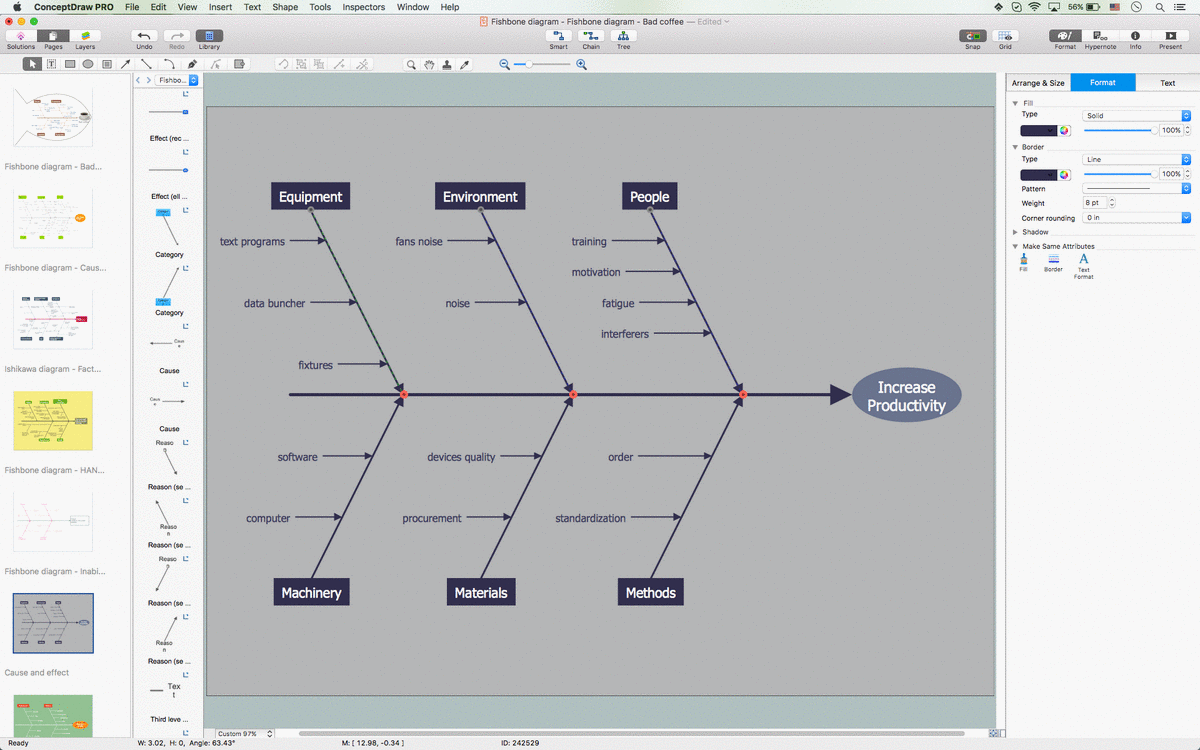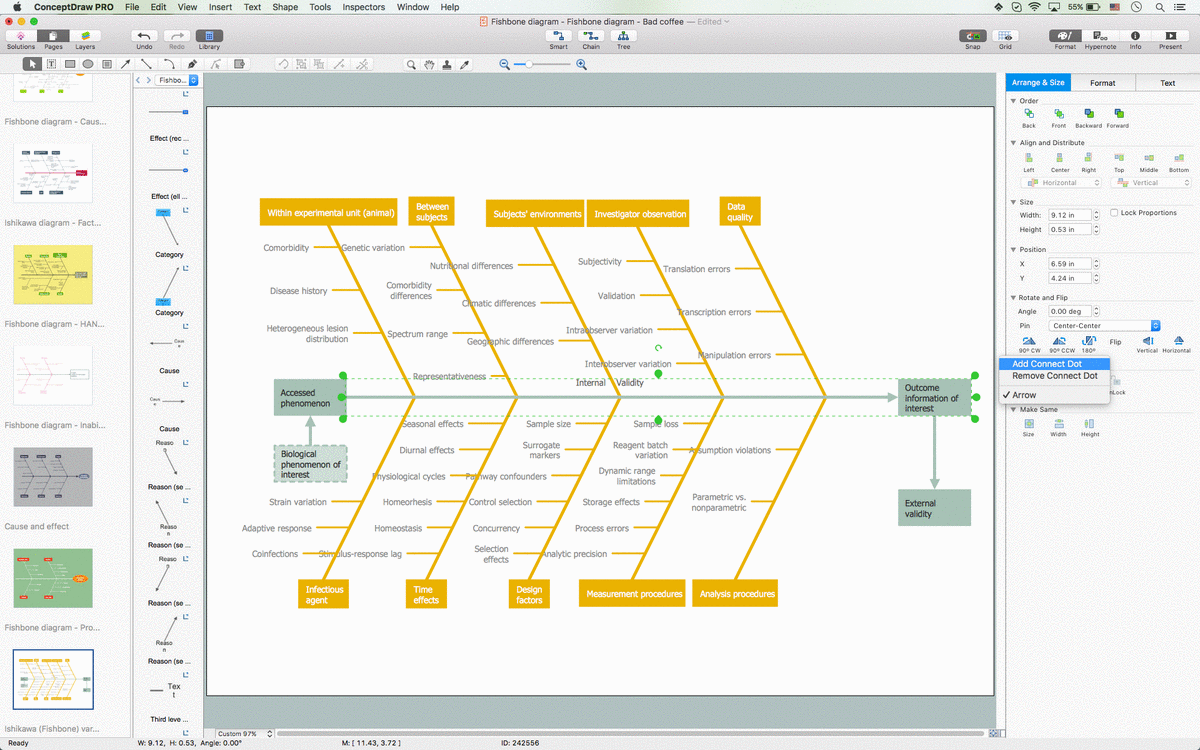
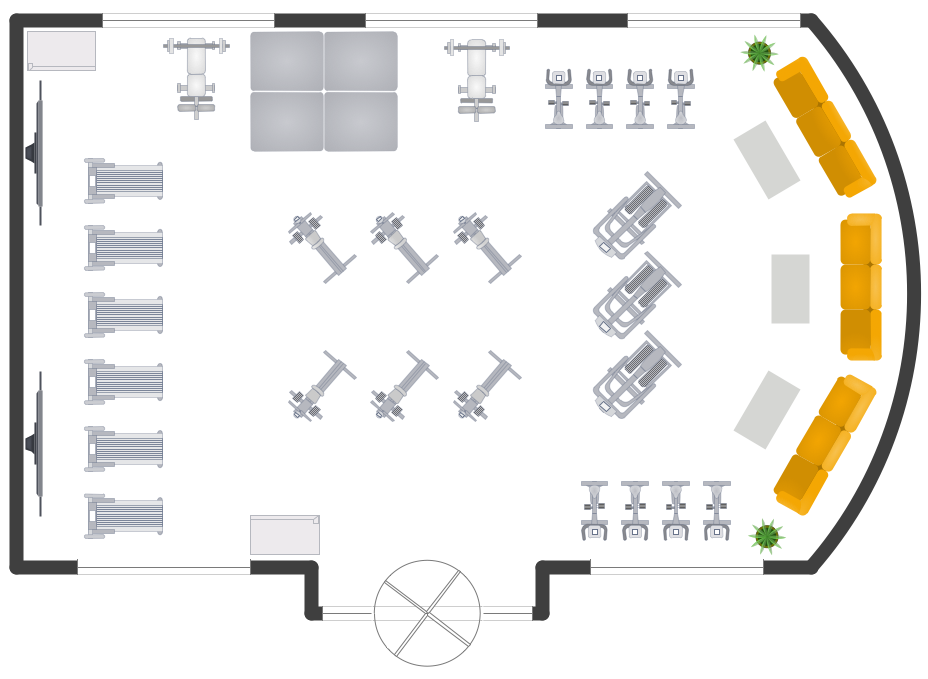
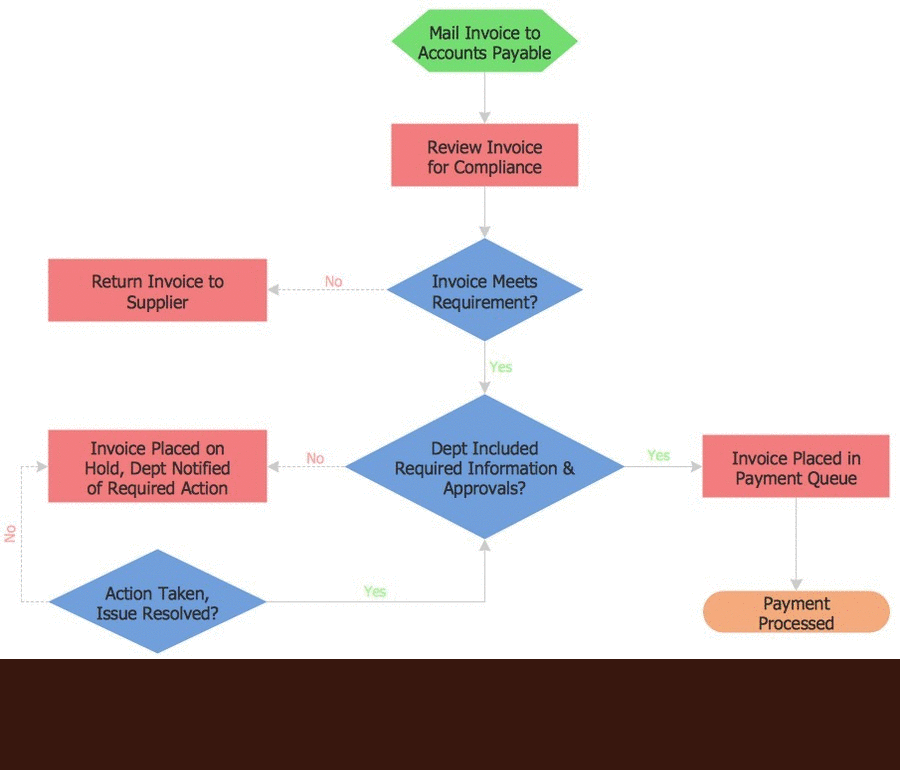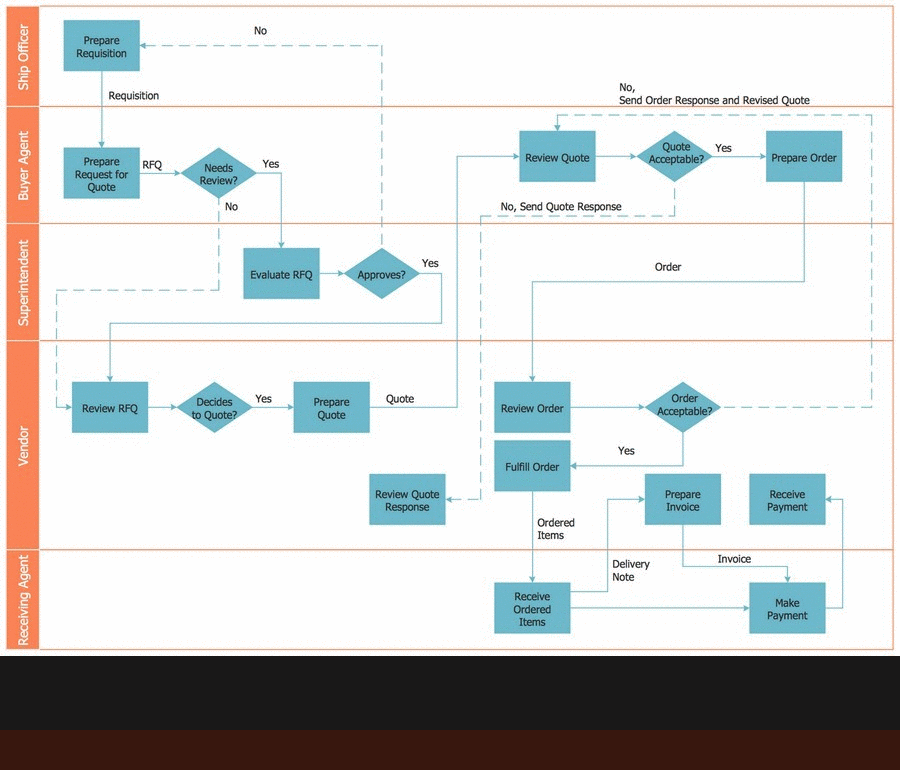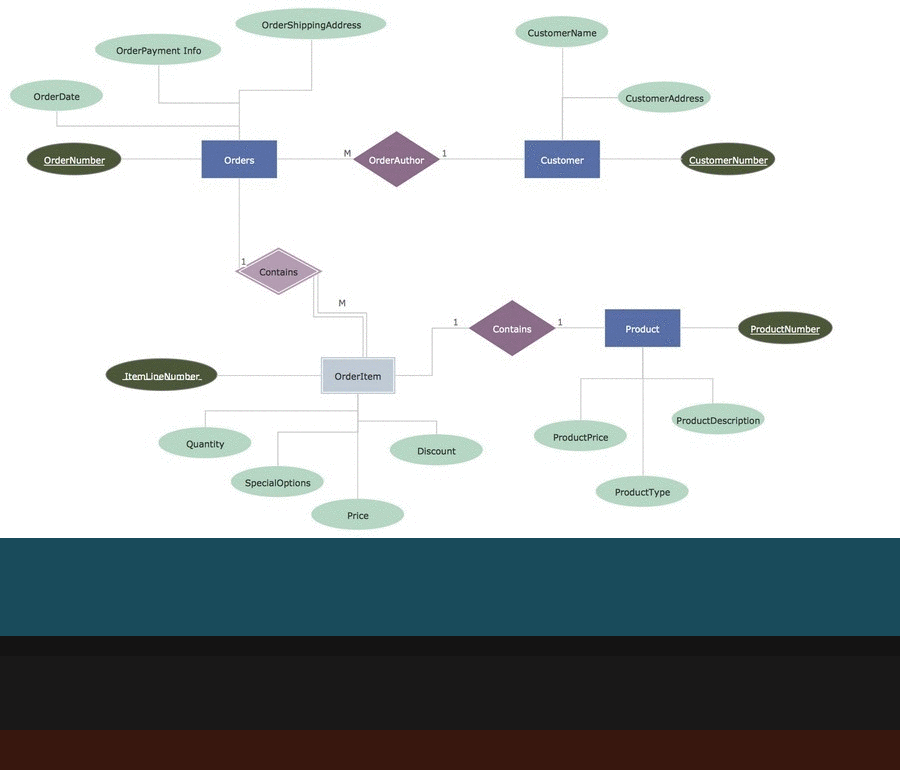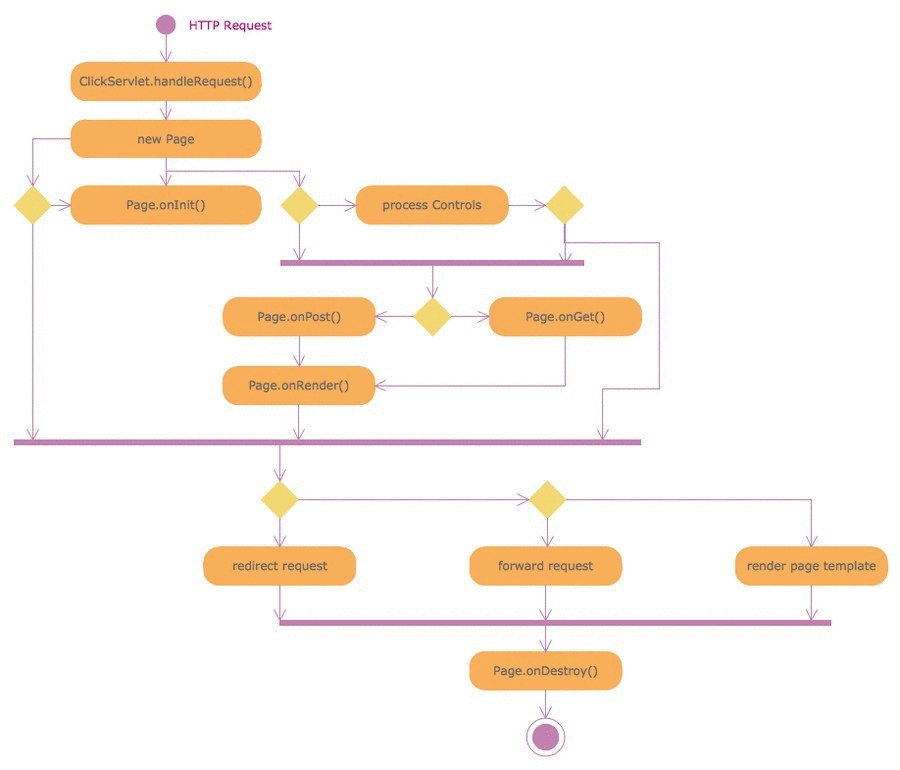
Example 1. Finite State Machine (FSM) Diagram

Finite state machines are widely used in systems engineering, system design, in developing computer programs and sequential logic circuits. Specification and Description Language (SDL) Solution offers all needed tools for designing without efforts. These are the SDL Connnectors and SDL Diagrams libraries which contain numerous predesigned vector objects, collection of FSM and SDL samples represented in ConceptDraw STORE.

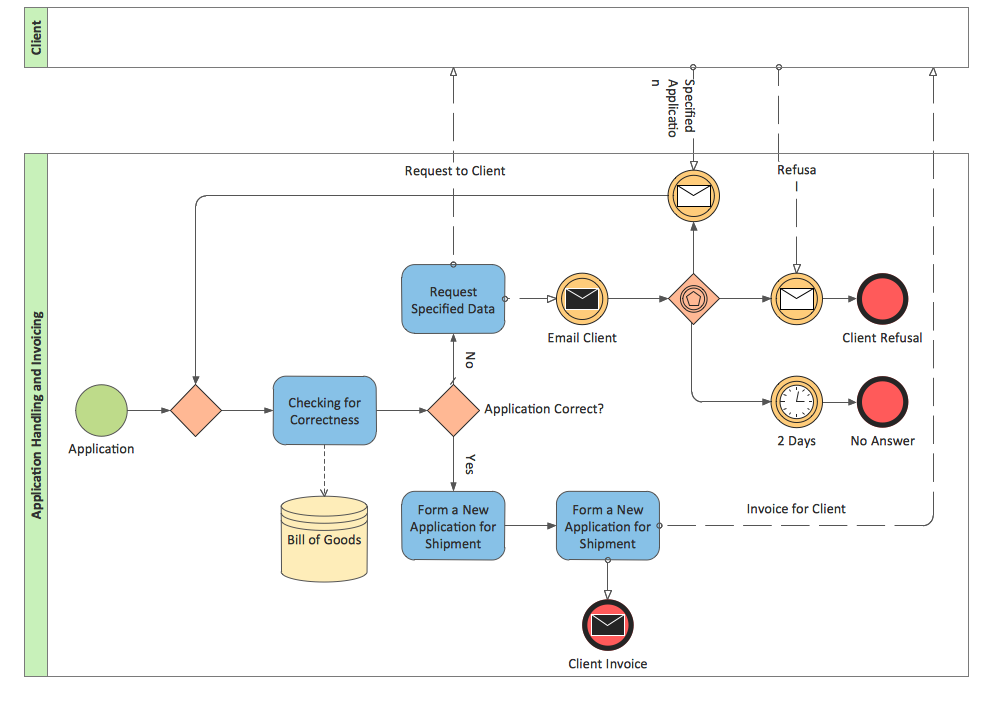
Example 2. Specification and Description Language (SDL) Solution in ConceptDraw STORE

All samples included in Specification and Description Language (SDL) Solution are well thought-out and professionaly designed. You can choose any desired of them from ConceptDraw STORE, it will be automatically opened in ConceptDraw DIAGRAM Then you are able to change some details in it or use the sample as the base for your own FSM diagram.

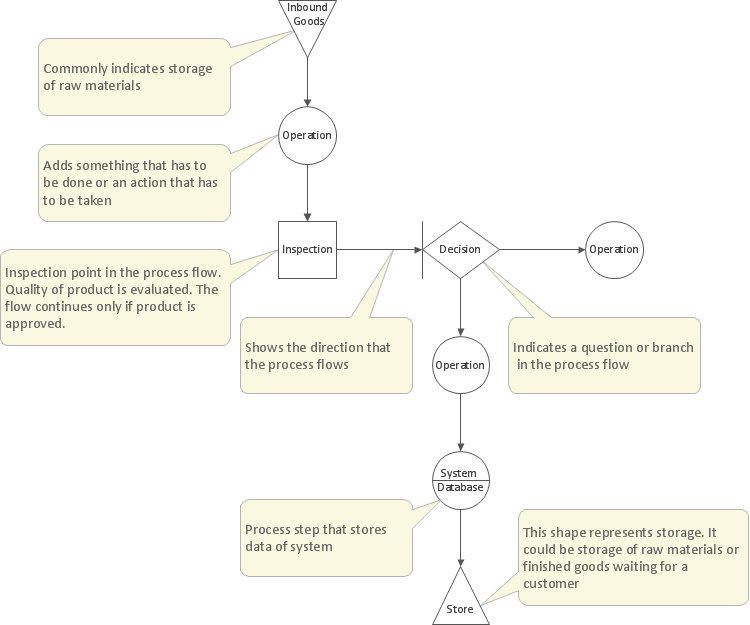
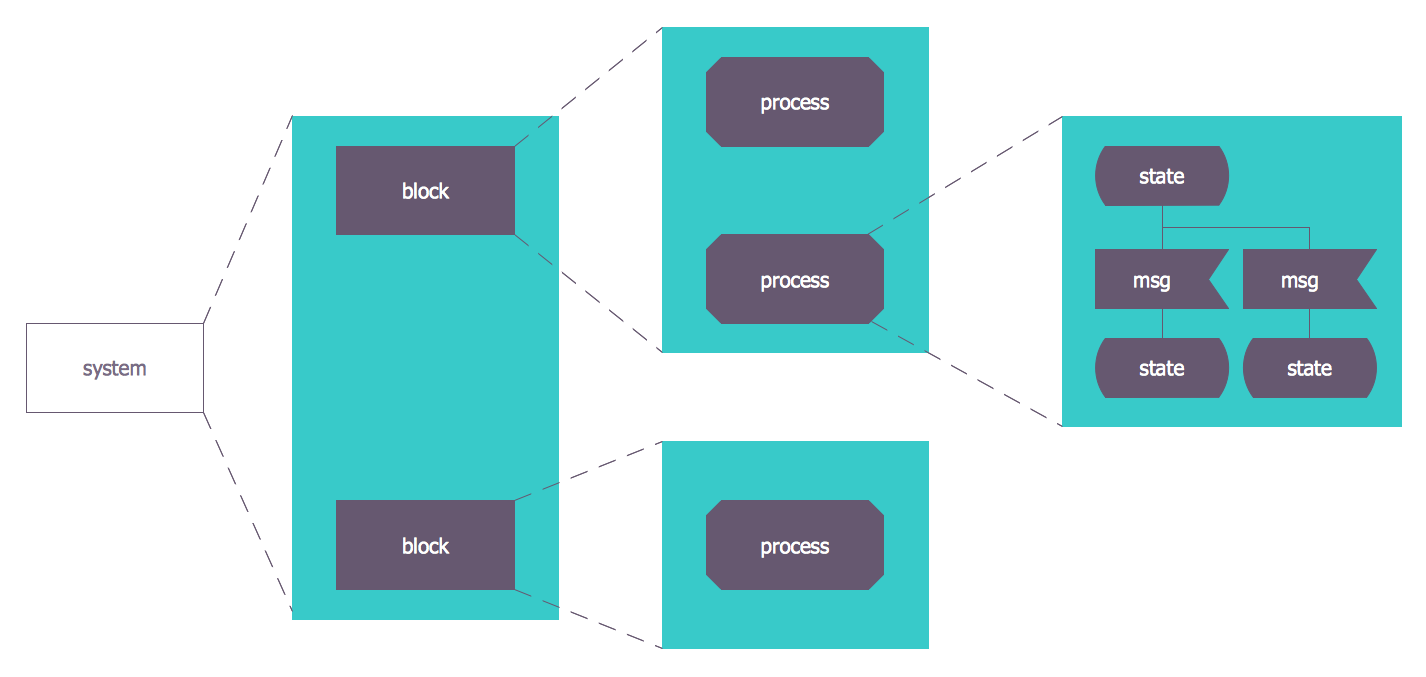
Example 3. SDL Architecture

The samples you see on this page were created in ConceptDraw DIAGRAM software using the tools of Specification and Description Language (SDL) Solution. First of them demonstrates the Finite State Machine (FSM) diagram, the second represents the SDL architecture and describes the processes within the sub-blocks also with help of finite state machines. An experienced user spent 10-20 minutes creating each of these samples.

Use the Specification and Description Language (SDL) Solution for ConceptDraw DIAGRAM software to create your own professional looking FSM and SDL diagrams fast, easy and effective.

All source documents are vector graphic documents. They are available for reviewing, modifying, or converting to a variety of formats (PDF file, MS PowerPoint, MS Visio, and many other graphic formats) from the ConceptDraw STORE. The Specification and Description Language (SDL) Solution is available for all ConceptDraw DIAGRAM users.