Venn Diagram Examples for Problem Solving

Computer Science. Chomsky Hierarchy

Venn diagram going by such nicknames as “primary diagram”, “set diagram” or “logic diagram” is widely known. This kind of diagram shows all possible logical relations between a finite collection of different sets. These diagrams depict the elements as points in the plane as well as sets of the regions inside the closed curves. A “Venn diagram” consists of the multiple overlapping closed curves, which are usually represented in the circles, each of which represents a set. The points inside a curve labeled “S” represent all of the elements of the set “S” and the points outside the boundary represent all of the other elements, but in the set “S”.

In “Venn diagrams” the curves are overlapped in different ways, showing all possible relations between the existing sets. This kind of diagrams was invented in the year of 1880 in a paper work named “On the Diagrammatic and Mechanical Representation of Propositions and Reasonings” by John Venn in the "Philosophical Magazine and Journal of Science" and they are used to teach elementary of the “set theory”, as well as to illustrate the simple set relationships in logic, linguistics, probability and computer science. Venn never used the term "Venn diagram" and he referred to his invention as “Eulerian Circles”. An “area-proportional” or “scaled” Venn diagram is the Venn diagram in which the area of each of the shapes is proportional to the number of elements which it contains.

Venn diagrams in general are very similar to the “Euler diagrams”, which were invented by Leonhard Euler in the 18th century. Baron has noted that Leibniz in the 17th century produced similar diagrams before Euler, most of which was unpublished. In the 20th century, Venn diagrams were better developed and in 1963 D. W. Henderson showed that the existence of an n-Venn diagram with n-fold “rotational symmetry” implied that n was a “prime number”, which means a natural number greater than 1 that has no positive divisors other than 1 and itself.

D. W. Henderson also showed that symmetric Venn diagrams exist when n is 5 or 7. In the year of 2002 Peter Hamburger found symmetric Venn diagrams for n = 11 and in 2003, Griggs, Killian and Savage showed that symmetric Venn diagrams exist for all other primes. Thus, rotationally symmetric Venn diagrams exist if “n” is a “prime number”. “Venn diagrams” and “Euler diagrams” were incorporated in the 1960s as part of instruction in so-called “set theory” as part of the “new math movement”. Since then, they have also been adopted in the curriculum of other fields.

A Venn diagram is built using a collection of simple closed curves in a plane. The principle of these diagrams is that classes (also known as “sets”) can be represented by regions in such relation to one another that all the possible logical relations of these classes (or “sets”) can be indicated in the same diagram. That is, the diagram initially leaves room for any possible relation of the classes. The actual or given relation within this diagram can be specified by indicating that some particular region is null or is not-null.

Venn diagrams normally comprise the overlapping circles. The inner part of the circle with the aid of the symbols represents the elements of the set. The exterior, though, implies elements that are not included into of the set. For example, in a two-set Venn diagram, one circle may represent the group of all objects made of wood, while another circle may represent the set of all tables. The overlapping region would then represent the set of all wooden tables. Any other shapes, but circles, can be employed as shown below by Venn's own higher set diagrams.

Venn diagrams do not contain the information on the relative or absolute sizes of sets and they are similar to “Euler diagrams”, as mentioned before. However, a Venn diagram for “n” component sets must contain all 2n hypothetically possible zones which correspond to some combination of inclusion (or exclusion) in each of the component sets.

The difference between the “Euler diagrams” and the “Venn diagrams” is that the “Euler diagrams” contain only the actually possible zones in a given context. In “Venn diagrams”, though, a shaded zone may represent an empty zone. At the same time in the “Euler diagrams” the corresponding zones are missing from the diagrams. As an example, you can imagine one set representing dairy products and another one – cheeses. In this case the “Venn diagram” contains a zone for cheeses that are not dairy products. Thus, the context cheese means some type of dairy product, the “Euler diagram” has the cheese zone entirely contained within the dairy-product one as there is no zone for non-dairy cheese. In this case the “Euler diagrams” are typically less visually complex than similar to them “Venn diagrams”, especially if the number of non-empty intersections is small.

Once you plan to draw any of the mentioned above diagrams, including the “Venn” ones, then you can find ConceptDraw DIAGRAM a very useful tool that allows to make any needed drawings within a short period of time having all of the necessary tools, such as design elements and symbols, which are all always available for ConceptDraw DIAGRAM users: basic in the application and all the rest needed are there in solutions, which can be always downloaded from ConceptDraw STORE or from this site. You can always draw any “Venn diagram” for a purpose of the problem-solving in computer science using the ConceptDraw DIAGRAM diagramming and vector drawing software extended with the Business Diagrams solution. The Business Diagrams solution can be always downloaded from the Management area of ConceptDraw Solution Park on this site or from ConceptDraw STORE.

Example 1. Business Diagrams Solution

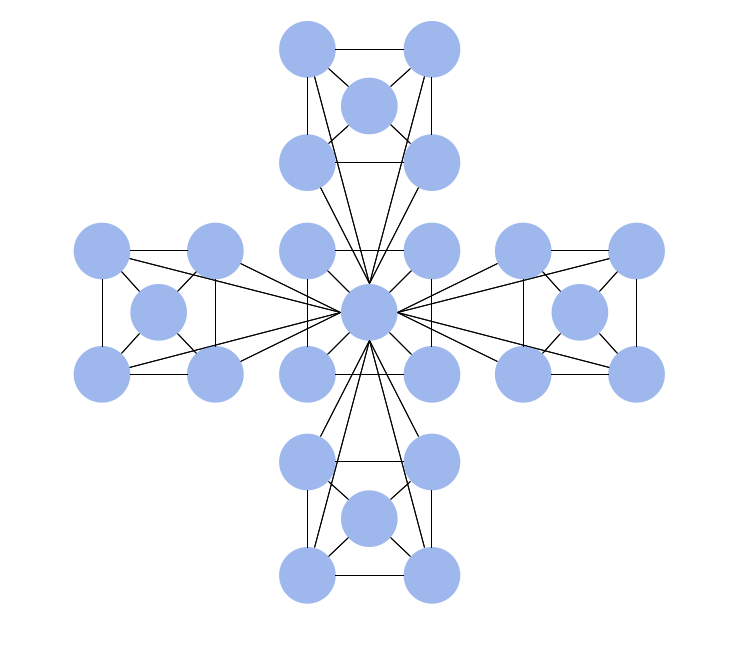
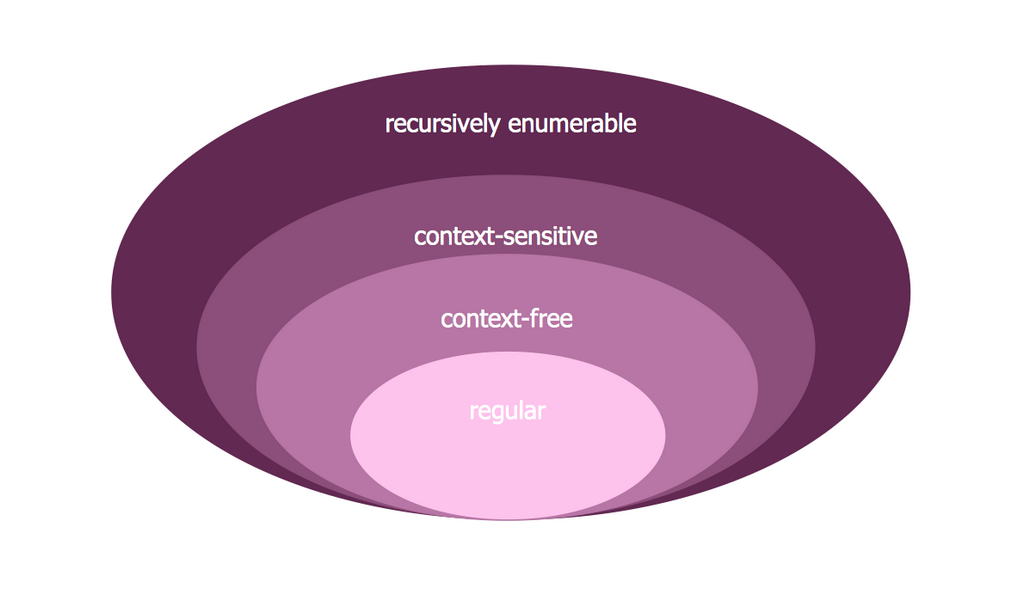
The Venn diagram example below visualizes the the class of language inclusions described by the Chomsky hierarchy.

"Within the field of computer science, specifically in the area of formal languages, the Chomsky hierarchy (occasionally referred to as Chomsky-Schützenberger hierarchy) is a containment hierarchy of classes of formal grammars. This hierarchy of grammars was described by Noam Chomsky in 1956. It is also named after Marcel-Paul Schützenberger, who played a crucial role in the development of the theory of formal languages. The Chomsky Hierarchy, in essence, allows the possibility for the understanding and use of a computer science model which enables a programmer to accomplish meaningful linguistic goals systematically." [Chomsky hierarchy. Wikipedia]

Example 2. Venn Diagram Problem Solving — Chomsky Hierarchy

A graphical representation of the sets of languages included in the Chomsky hierarchy.

"The Chomsky hierarchy consists of the following levels:

• Type-0 grammars (unrestricted grammars) include all formal grammars. They generate exactly all languages that can be recognized by a Turing machine. These languages are also known as the recursively enumerable languages.
• Type-1 grammars (context-sensitive grammars) generate the context-sensitive languages. ... The languages described by these grammars are exactly all languages that can be recognized by a linear bounded automaton (a nondeterministic Turing machine whose tape is bounded by a constant times the length of the input.)
• Type-2 grammars (context-free grammars) generate the context-free languages. ... These languages are exactly all languages that can be recognized by a non-deterministic pushdown automaton. Context-free languages – or rather the subset of deterministic context-free language – are the theoretical basis for the phrase structure of most programming languages, though their syntax also includes context-sensitive name resolution due to declarations and scope. Often a subset of grammars are used to make parsing easier, such as by an LL parser.
• Type-3 grammars (regular grammars) generate the regular languages."
  [Chomsky hierarchy. Wikipedia]

Having ConceptDraw DIAGRAM software as well as Business Diagrams solution one allows anyone who cares for their drawings to look not only nice but also smart and professional, to get the needed result in only a few hours or even minutes, depending on how familiar you are with ConceptDraw DIAGRAM