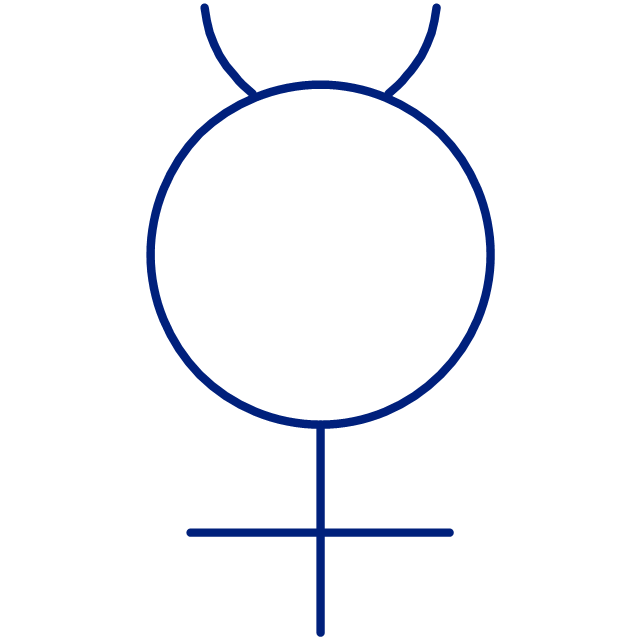
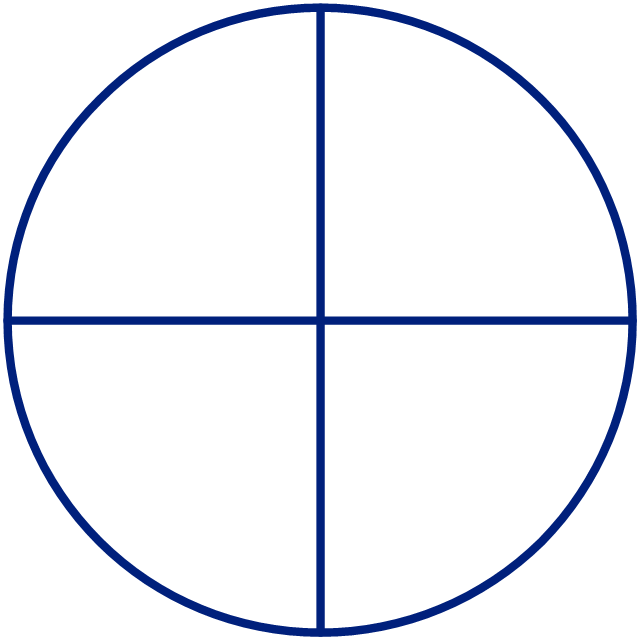
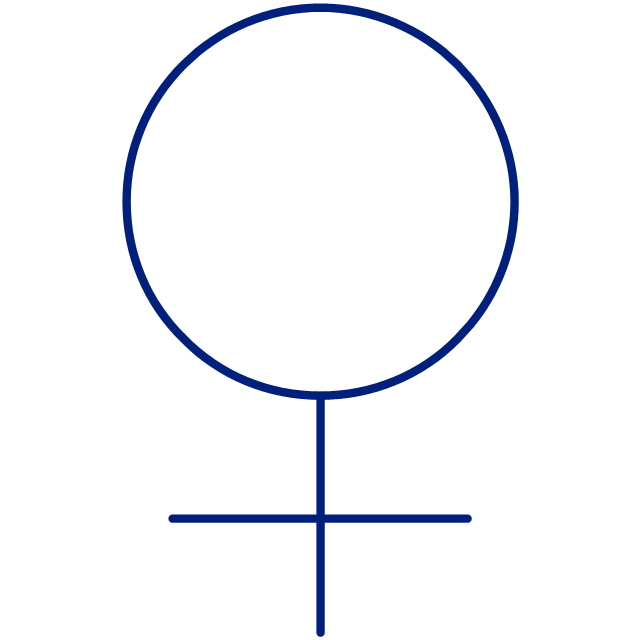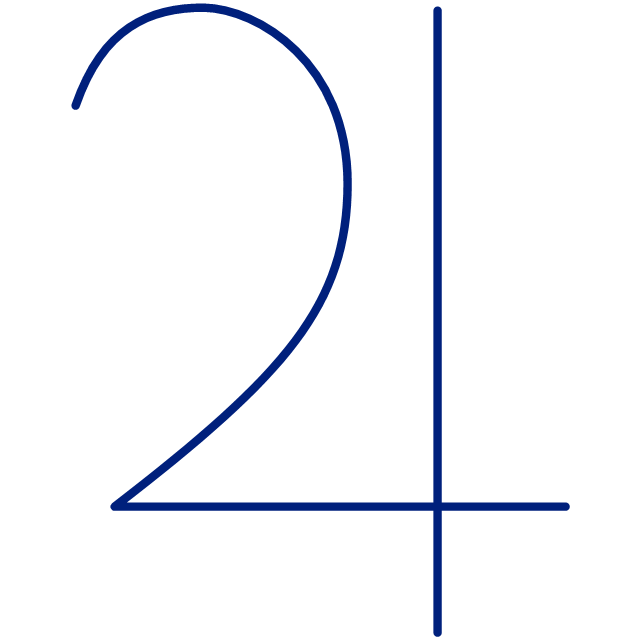Astronomy Symbols
Are you an astronomer, astronomy teacher or student? And you need to draw astronomy pictures quick and easy? ConceptDraw DIAGRAM diagramming and vector drawing software extended with Astronomy solution from the Science and Education area will help you! Astronomy solution provides 7 libraries with wide variety of predesigned vector objects of astronomy symbols, celestial bodies, solar system symbols, constellations, etc.The vector stencils library "Astronomical symbols" contains 58 astronomical symbols and astrological signs of Solar system planets, stars, Sun, Moon, Earth, constellations, Mercury, Venus, Mars, Saturn, Jupiter, Uranus, Neptune, comet, Zodiac signs.
"Astronomical symbols are symbols used to represent various celestial objects, theoretical constructs and observational events in astronomy. The earliest forms of these symbols appear in Greek papyri of late antiquity. The Byzantine codices in which the Greek papyri were preserved continued and extended the inventory of astronomical symbols. New symbols were further invented to represent many just-discovered planets and minor planets discovered in the 18th-20th centuries.
All these symbols were once commonly used by professional astronomers, amateur astronomers, and astrologers. While they are still commonly used in almanacs and astrological publications, their occurrence in published research and texts on astronomy is relatively infrequent, with some exceptions such as the Sun and Earth symbols appearing in astronomical constants, and certain zodiacal signs used to represent the solstices and equinoxes." [Astronomical symbols. Wikipedia]
The pictograms example "Design elements - Astronomical symbols" was created using the ConceptDraw PRO diagramming and vector drawing software extended with the Astronomy solution from the Science and Education area of ConceptDraw Solution Park.
"Astronomical symbols are symbols used to represent various celestial objects, theoretical constructs and observational events in astronomy. The earliest forms of these symbols appear in Greek papyri of late antiquity. The Byzantine codices in which the Greek papyri were preserved continued and extended the inventory of astronomical symbols. New symbols were further invented to represent many just-discovered planets and minor planets discovered in the 18th-20th centuries.
All these symbols were once commonly used by professional astronomers, amateur astronomers, and astrologers. While they are still commonly used in almanacs and astrological publications, their occurrence in published research and texts on astronomy is relatively infrequent, with some exceptions such as the Sun and Earth symbols appearing in astronomical constants, and certain zodiacal signs used to represent the solstices and equinoxes." [Astronomical symbols. Wikipedia]
The pictograms example "Design elements - Astronomical symbols" was created using the ConceptDraw PRO diagramming and vector drawing software extended with the Astronomy solution from the Science and Education area of ConceptDraw Solution Park.
HelpDesk
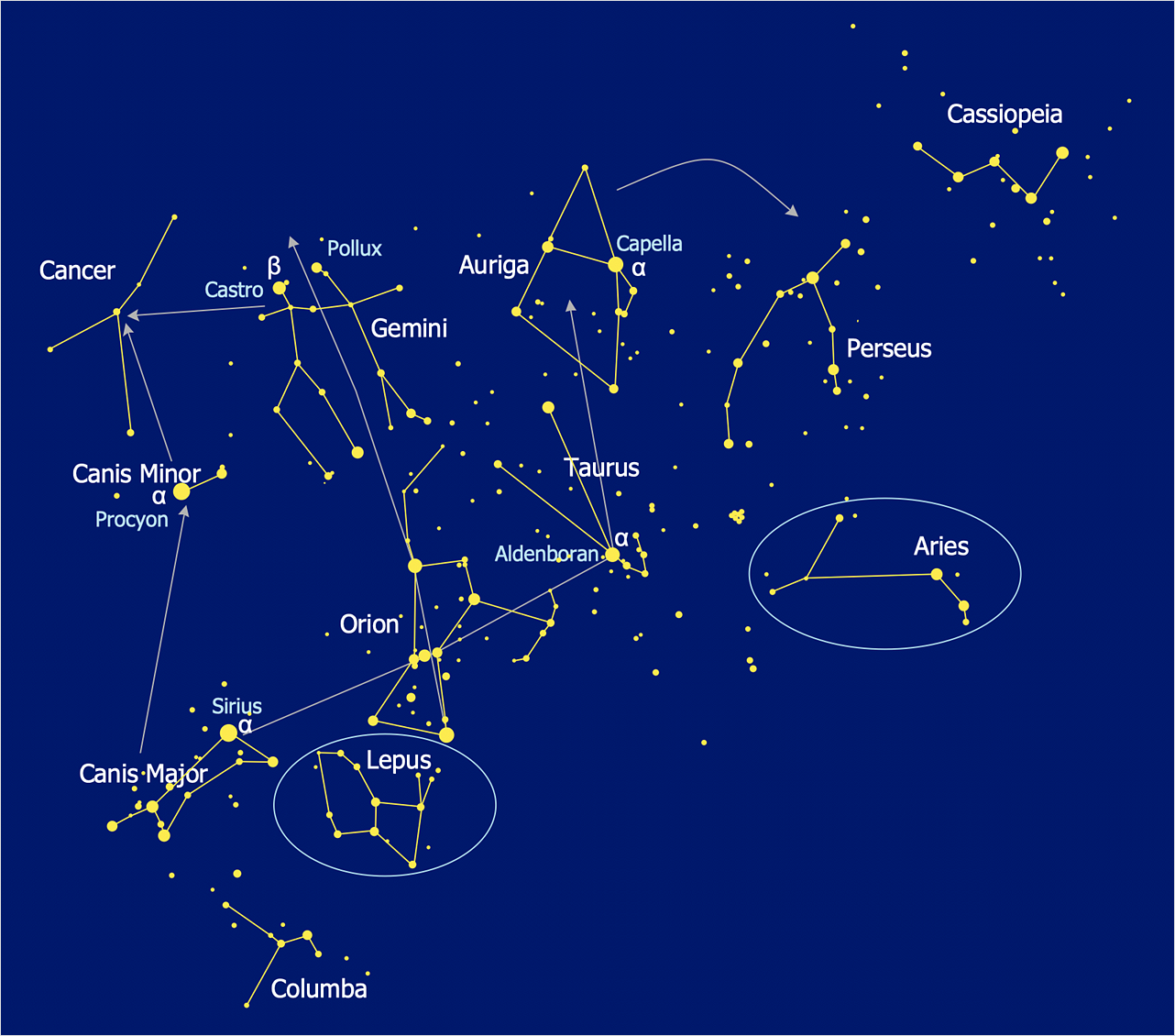
How to Draw a Сonstellation Сhart
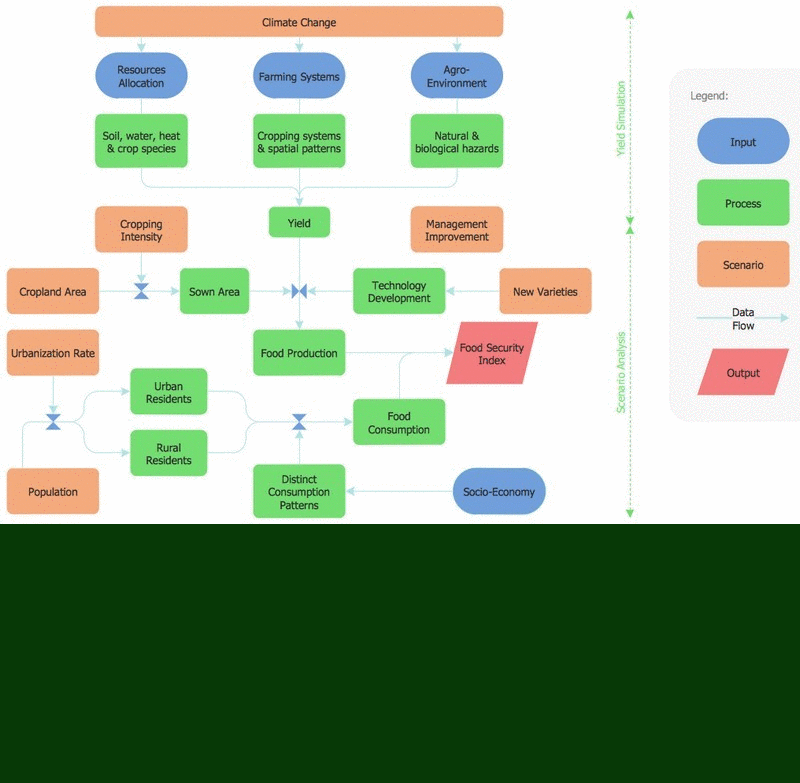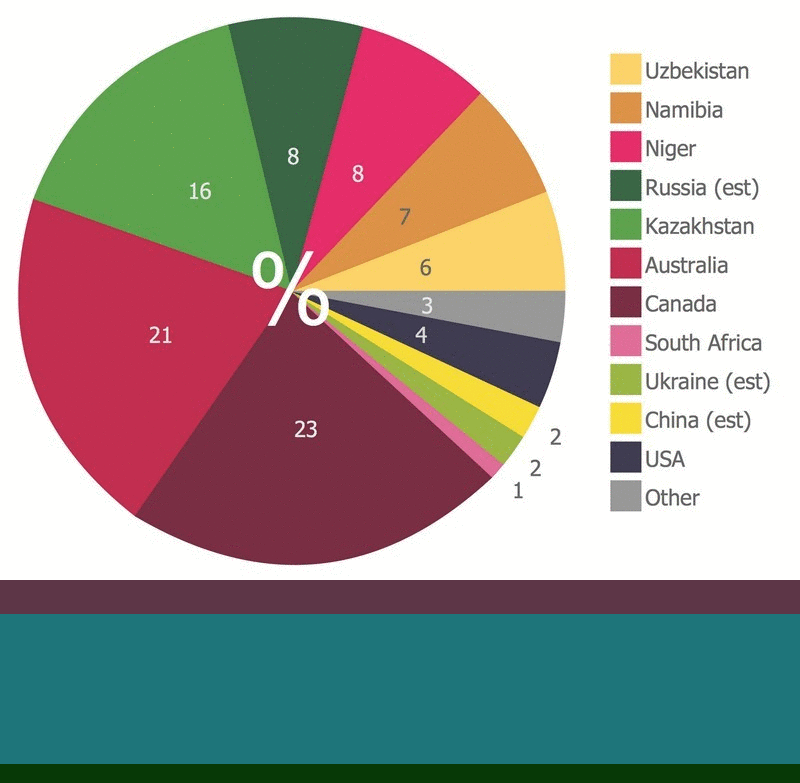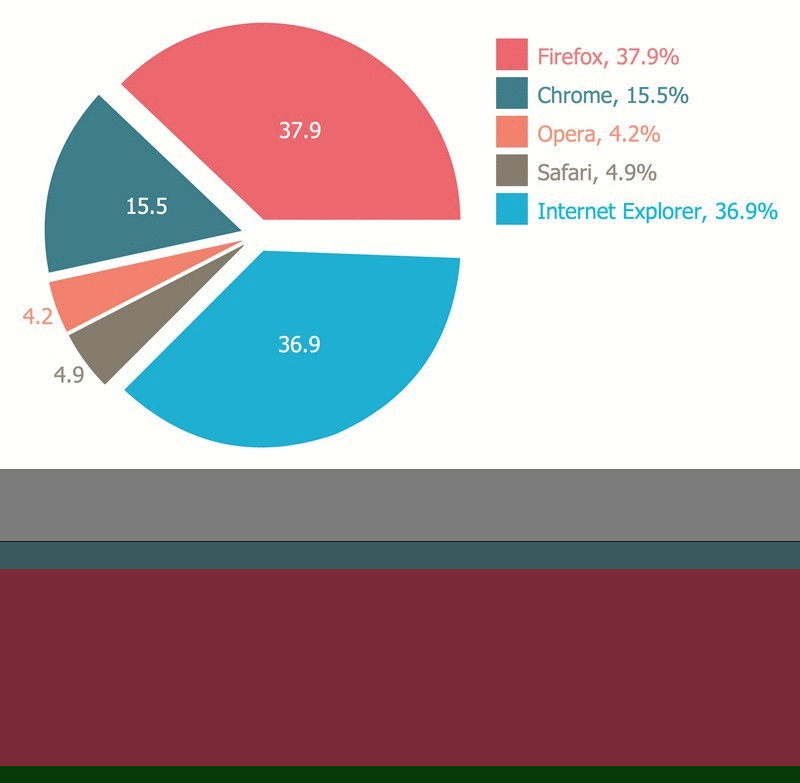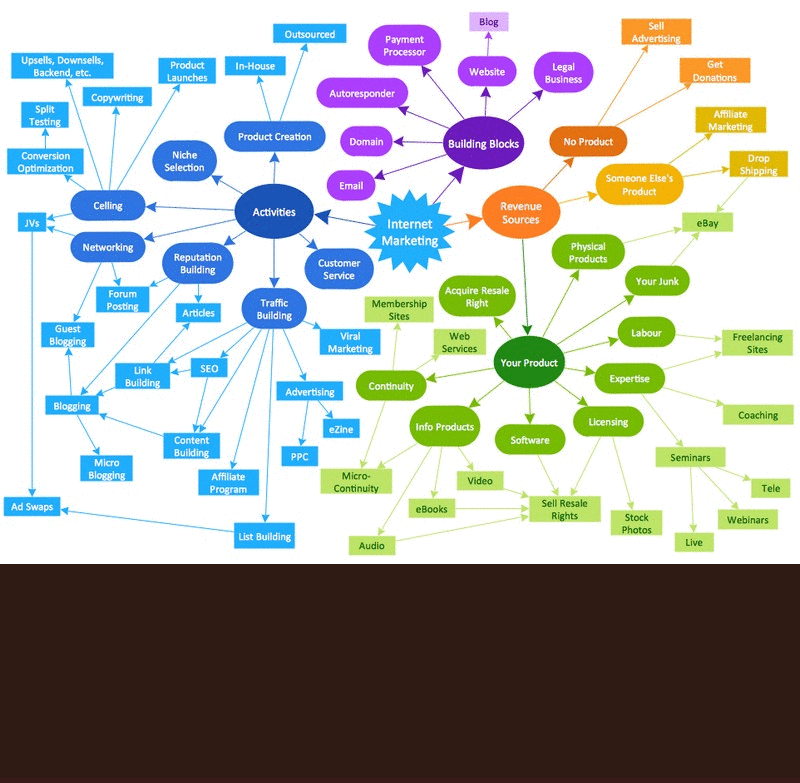
Astronomic maps are used to locate stars, planets and other objects in the sky for a certain date, time and observing location. ConceptDraw Astronomy solution can be used as a tool for creating astronomy maps, charts and illustrations that contains astronomy symbols of constellations, galaxies, stars and planets. It allows you to draw the map of any constellation quickly and easily using the special templates and vector stencils libraries.Physics Symbols
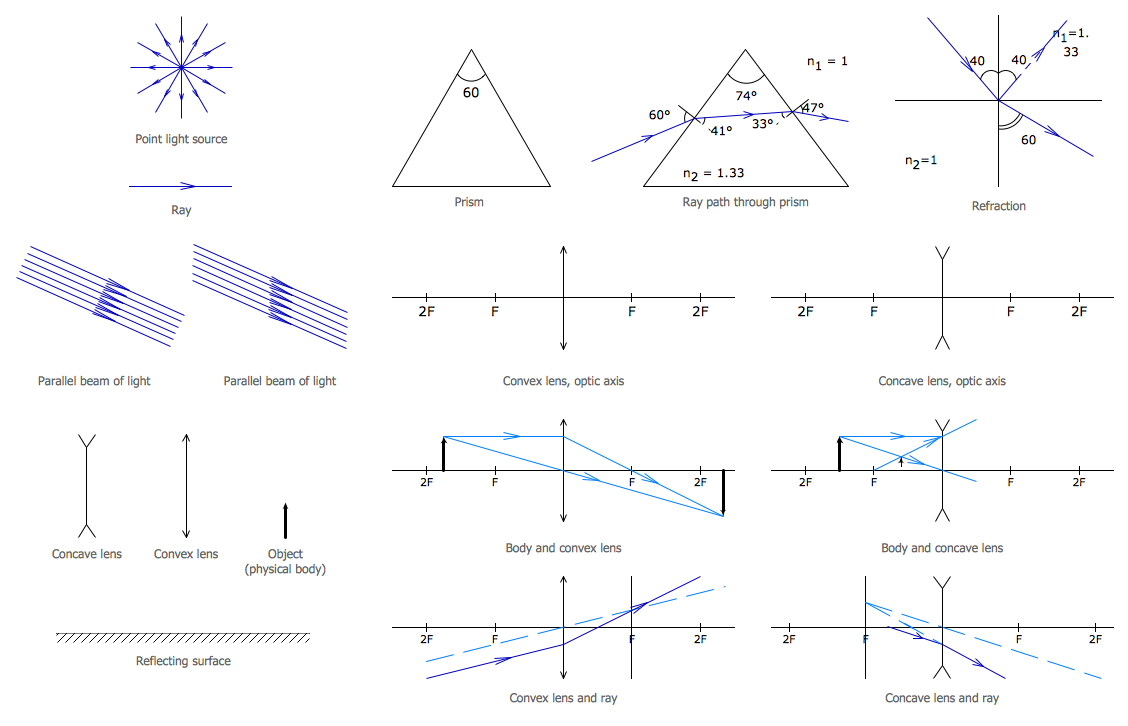
ConceptDraw DIAGRAM diagramming and vector drawing software extended with Physics solution from the Science and Education area is a powerful software for creating various physics diagrams. Physics solution provides all tools that you can need for physics diagrams designing. It includes 3 libraries with predesigned vector physics symbols: Optics Library, Mechanics Library and Nuclear Physics Library.Biology Symbols
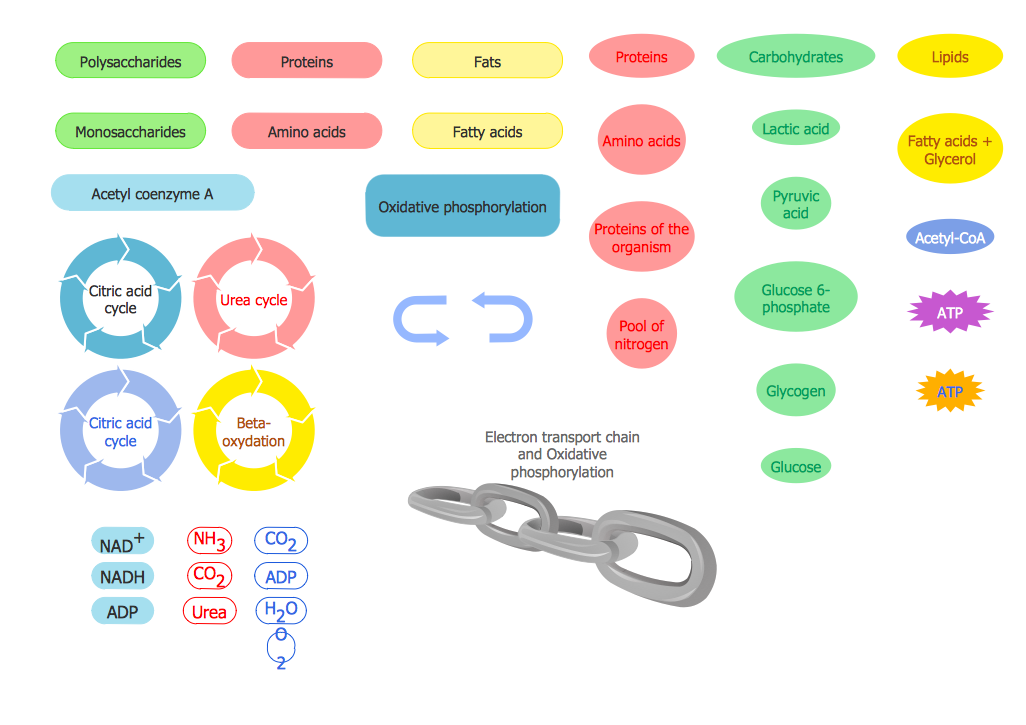
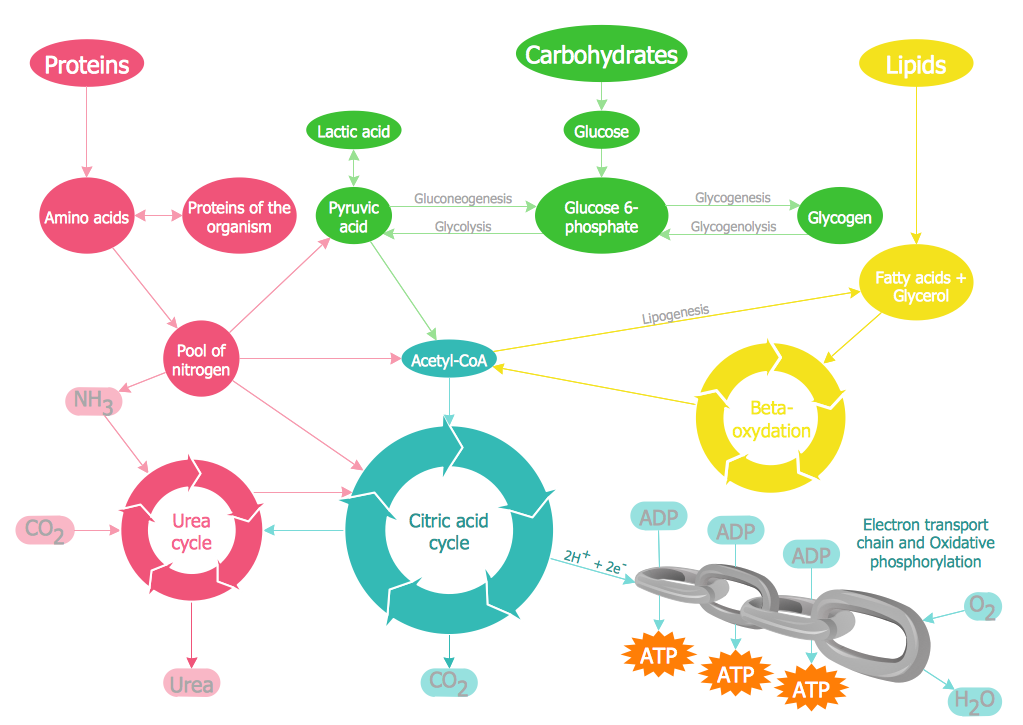
ConceptDraw DIAGRAM diagramming and vector drawing software extended with Biology solution from the Science and Education area offers a set of useful tools for fast and easy drawing of various biology illustrations and drawings.Biology solution provides 3 libraries with large quantity of vector biology symbols: Biochemistry of Metabolism Library, Carbohydrate Metabolism Library, Citric Acid Cycle (TCA Cycle) Library.
Sketching Software
ConceptDraw DIAGRAM is a powerful diagramming, vector drawing and sketching software that can be successfully used for creating various sketches, illustrations, drawing in any field of science and life activity. In particular, ConceptDraw DIAGRAM offers the Astronomy solution from the Science and Education area to help you design the astronomy pictures, sun solar system drawings, constellation chart quick and easy.Best Program to Make Diagrams
Make diagrams, charts, workflows, flowcharts, org charts, project charts easily with ConceptDraw software.
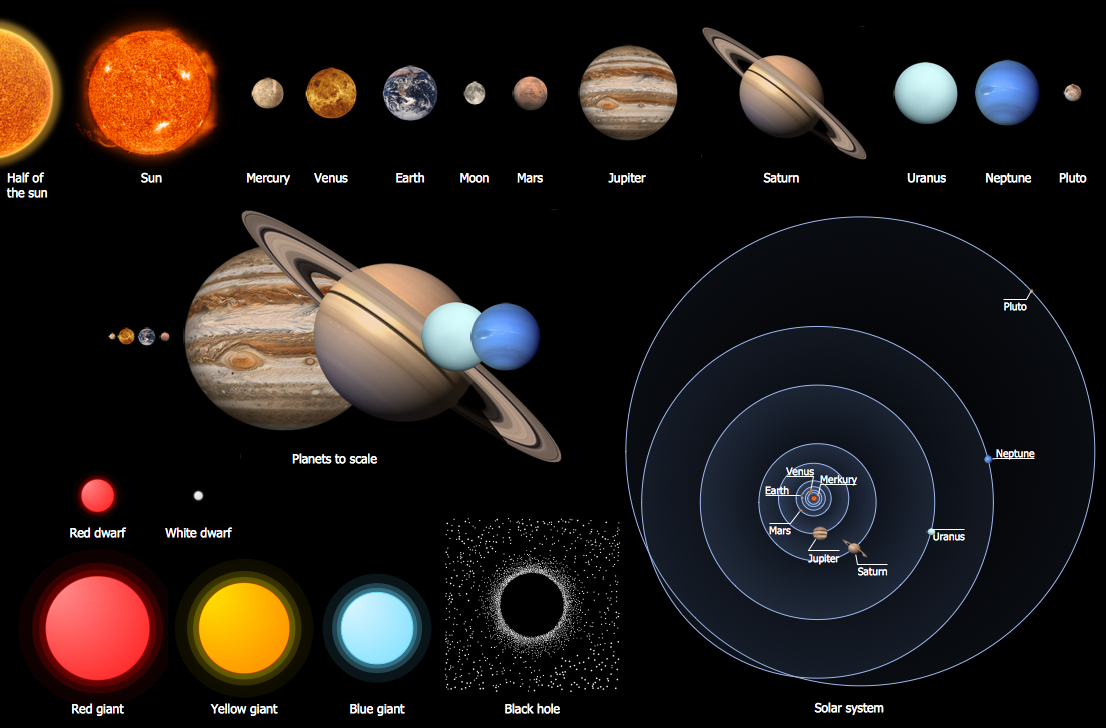
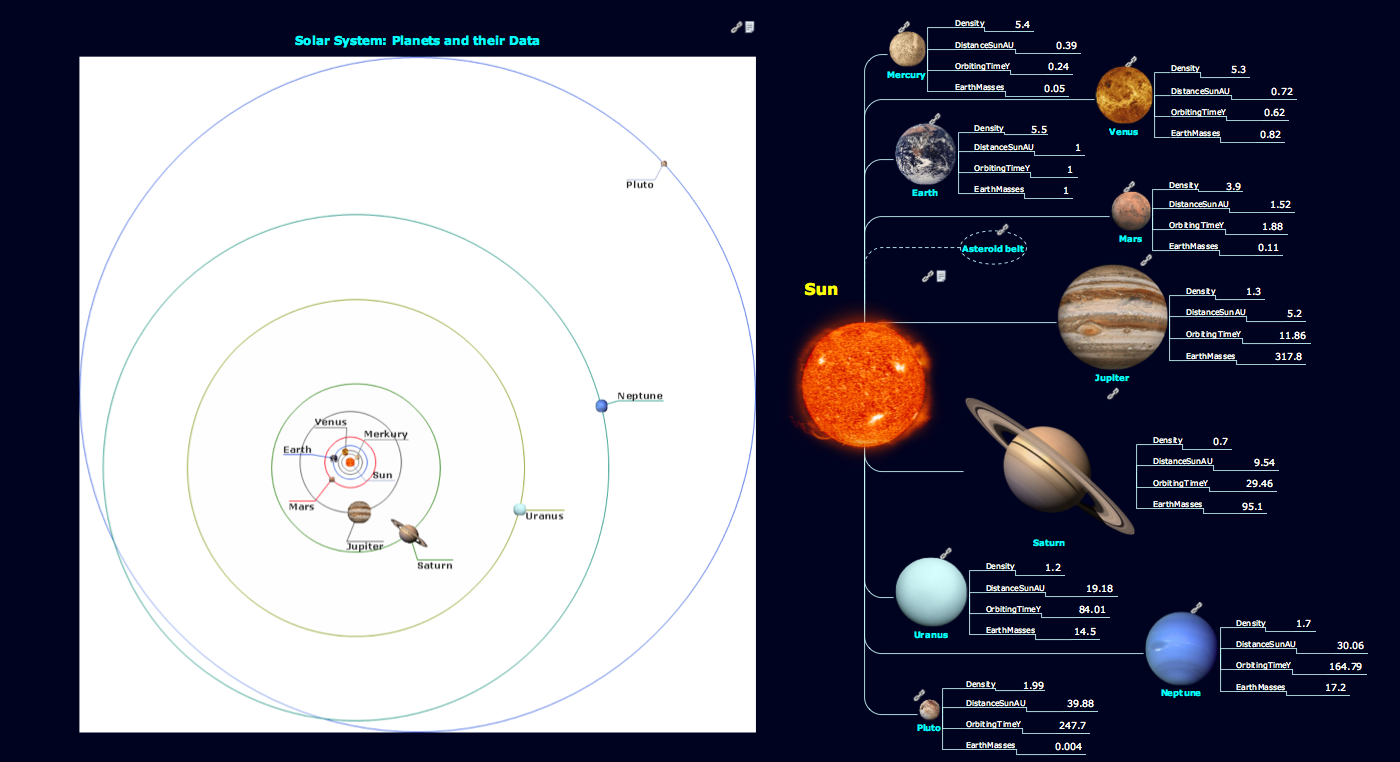
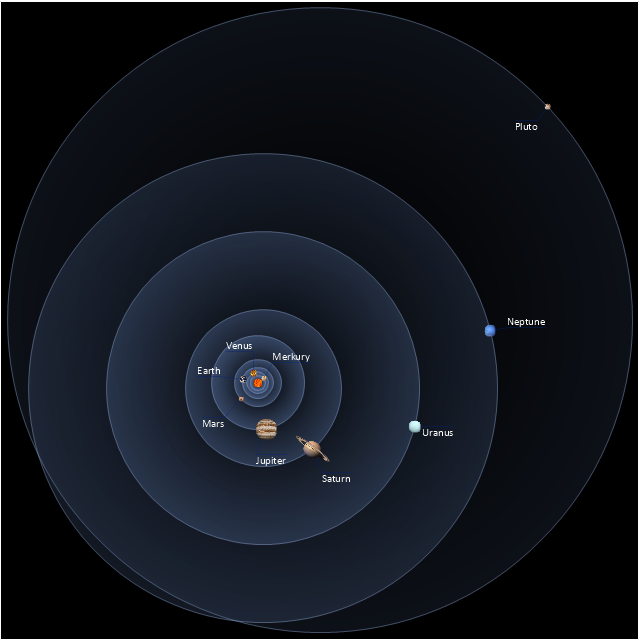
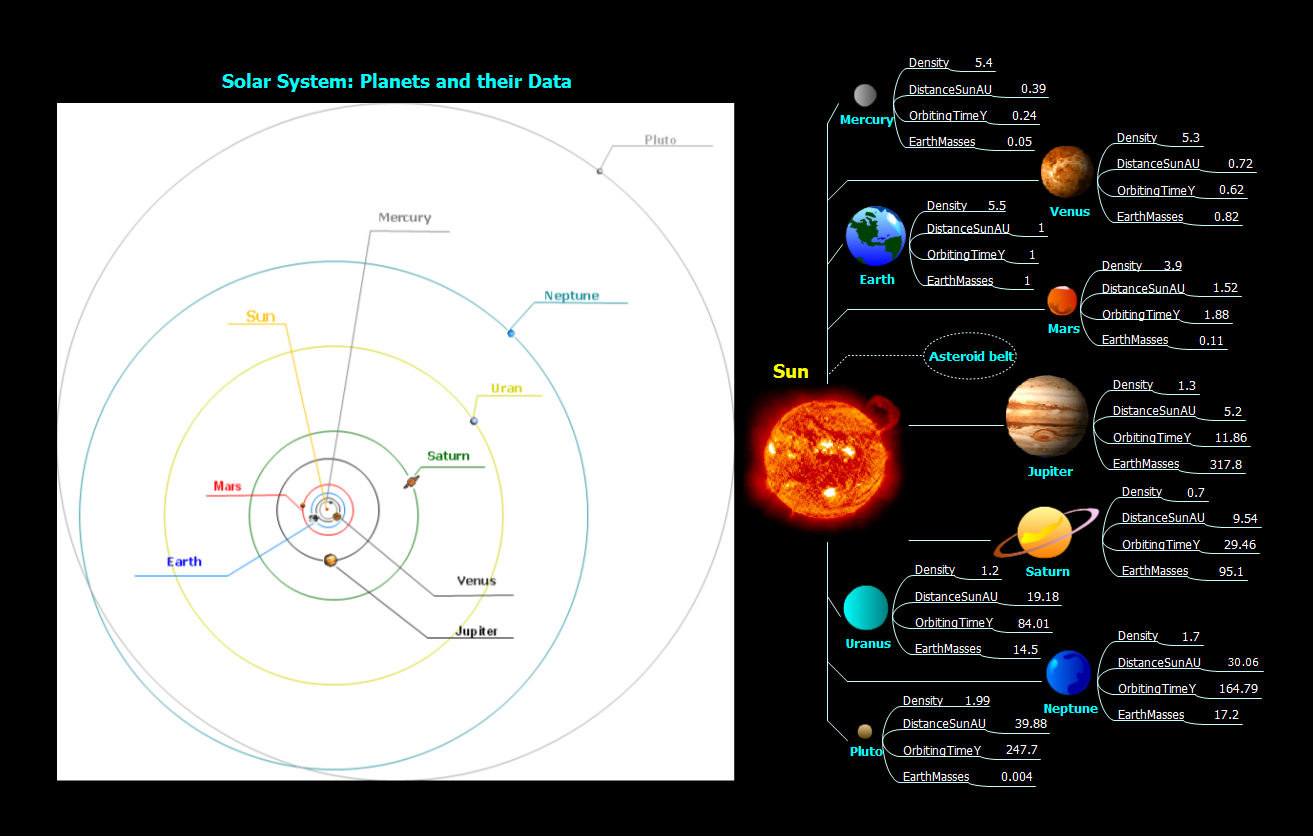
Solar System Symbols
Astronomy solution provides the Stars and Planets library with wide variety of solar system symbols. You can find here vector objects of solar system, of stars and planets of the universe. To quickly draw any astronomy illustration: create new document and simply drag the needed solar system symbols from the Stars and Planets library, arrange them and add the text. You can also use the predesigned templates and samples from the ConceptDraw STORE as the base for your own sun solar system illustrations, astronomy and astrology drawings.Biology Illustration
Biology solution offers 3 libraries of ready-to-use predesigned biology symbols and vector clipart to make your biology drawing and biology illustration making fast and easy: Carbohydrate Metabolism Library, Biochemistry of Metabolism Library, Citric Acid Cycle (TCA Cycle) Library.Illustration Software
No science can't exist without illustrations, and especially astronomy! Illustrations help to visualize knowledge, natural phenomenons which are studied by astronomy, they equally effective help in work, during the learning process and on the conferences. Now we have professional astronomy illustration software - ConceptDraw DIAGRAM illustration and sketching software with templates, samples and libraries of a variety of astronomy symbols, including constellations, galaxies, stars, and planet vector shapes; a whole host of celestial bodies. When drawing scientific and educational astronomy illustrations, astronomy pictures and diagrams, can help you reach for the stars!Astronomy and Astrology
Astronomy and astrology require from the specialists permanent drawing wide variety of illustrations, sketches. It’s convenient for astronomers and astrologers to have software that will help design them quick and easy. ConceptDraw DIAGRAM diagramming and vector drawing software extended with Astronomy solution from the Science and Education area is exactly what they need.Sun Solar System
ConceptDraw DIAGRAM diagramming and vector drawing software offers the Astronomy solution with useful tools for drawing all kinds of astronomy pictures and sun solar system illustrations. The astronomy illustrations designed with ConceptDraw DIAGRAM are vector graphic documents and are available for reviewing, modifying, converting to a variety of formats (image, HTML, PDF file, MS PowerPoint Presentation, Adobe Flash or MS Visio XML), printing and send via e-mail in one moment.
 Astronomy
Astronomy
Astronomy solution extends ConceptDraw DIAGRAM software with illustration and sketching software with templates, samples and libraries of a variety of astronomy symbols, including constellations, galaxies, stars, and planet vector shapes; a whole host of cele
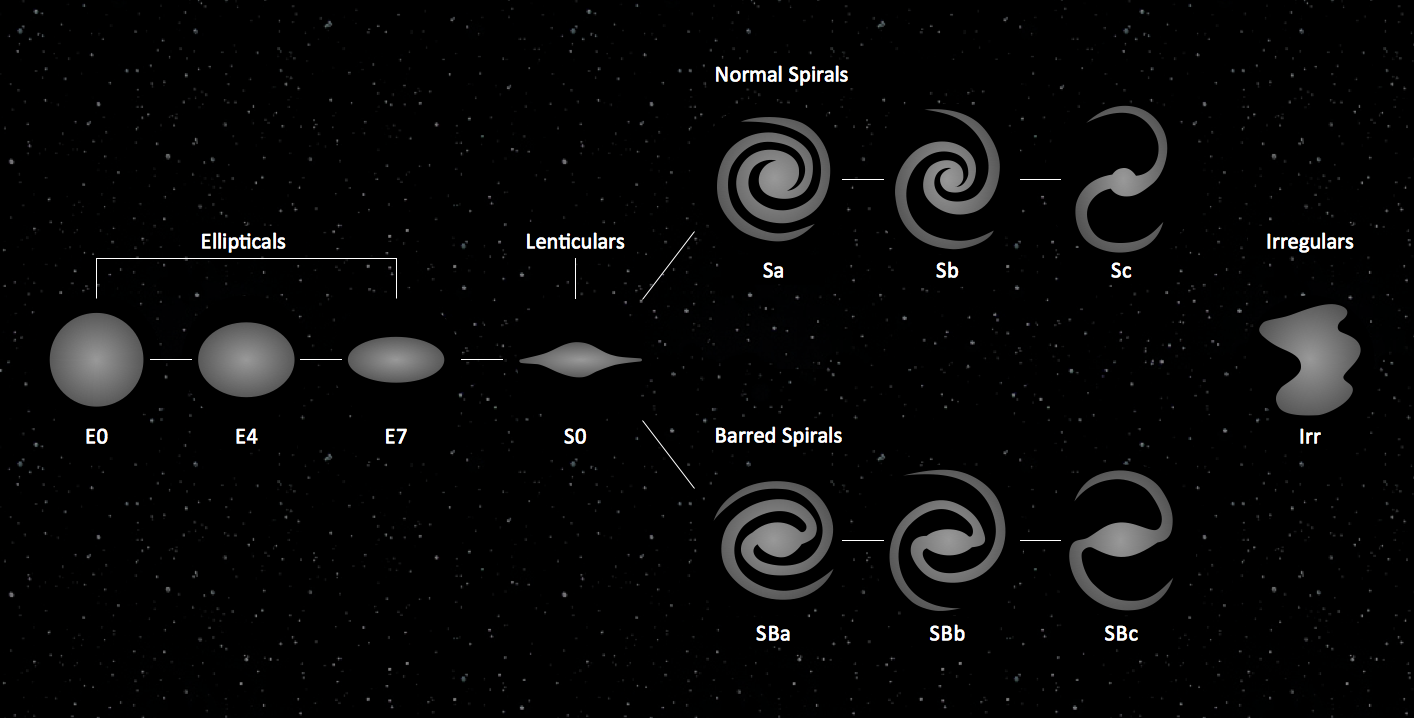
The vector stencils library "Galaxies" contains 15 galaxy symbols for drawing astronomical diagrams.
"A galaxy is a massive, gravitationally bound system consisting of stars, stellar remnants, an interstellar medium of gas and dust, and dark matter, an important but poorly understood component. The word galaxy is derived from the Greek galaxias ..., literally "milky", a reference to the Milky Way. Examples of galaxies range from dwarfs with as few as ten million (10^7) stars to giants with one hundred trillion (10^14) stars, each orbiting their galaxy's own center of mass.
Galaxies contain varying numbers of planets, star systems, star clusters and types of interstellar clouds. In between these objects is a sparse interstellar medium of gas, dust, and cosmic rays. Supermassive black holes reside at the center of most galaxies. They are thought to be the primary driver of active galactic nuclei found at the core of some galaxies. The Milky Way galaxy is known to harbor at least one such object.
Galaxies have been historically categorized according to their apparent shape, usually referred to as their visual morphology. A common form is the elliptical galaxy, which has an ellipse-shaped light profile. Spiral galaxies are disk-shaped with dusty, curving arms. Those with irregular or unusual shapes are known as irregular galaxies and typically originate from disruption by the gravitational pull of neighboring galaxies. Such interactions between nearby galaxies, which may ultimately result in a merger, sometimes induce significantly increased incidents of star formation leading to starburst galaxies. Smaller galaxies lacking a coherent structure are referred to as irregular galaxies."
[Galaxy. Wikipedia]
The example "Design elements - Galaxies" was created using the ConceptDraw PRO diagramming and vector drawing software extended with the Astronomy solution from the Science and Education area of ConceptDraw Solution Park.
"A galaxy is a massive, gravitationally bound system consisting of stars, stellar remnants, an interstellar medium of gas and dust, and dark matter, an important but poorly understood component. The word galaxy is derived from the Greek galaxias ..., literally "milky", a reference to the Milky Way. Examples of galaxies range from dwarfs with as few as ten million (10^7) stars to giants with one hundred trillion (10^14) stars, each orbiting their galaxy's own center of mass.
Galaxies contain varying numbers of planets, star systems, star clusters and types of interstellar clouds. In between these objects is a sparse interstellar medium of gas, dust, and cosmic rays. Supermassive black holes reside at the center of most galaxies. They are thought to be the primary driver of active galactic nuclei found at the core of some galaxies. The Milky Way galaxy is known to harbor at least one such object.
Galaxies have been historically categorized according to their apparent shape, usually referred to as their visual morphology. A common form is the elliptical galaxy, which has an ellipse-shaped light profile. Spiral galaxies are disk-shaped with dusty, curving arms. Those with irregular or unusual shapes are known as irregular galaxies and typically originate from disruption by the gravitational pull of neighboring galaxies. Such interactions between nearby galaxies, which may ultimately result in a merger, sometimes induce significantly increased incidents of star formation leading to starburst galaxies. Smaller galaxies lacking a coherent structure are referred to as irregular galaxies."
[Galaxy. Wikipedia]
The example "Design elements - Galaxies" was created using the ConceptDraw PRO diagramming and vector drawing software extended with the Astronomy solution from the Science and Education area of ConceptDraw Solution Park.
This vector stencils library contains 30 clipart images and astronomical symbols of sun and stars, solar system planets and moon.
Use these shapes for drawing your astronomical diagrams and illustrations.
Use these shapes for drawing your astronomical diagrams and illustrations.
Astronomy Pictures
Every day astronomers of the whole world and astronomy-related people draw wide variety of astronomy pictures, make the photos of various astronomic events, solar and planets activities. ConceptDraw DIAGRAM diagramming and vector drawing software extended with Astronomy solution from the Science and Education area is the best choice for astronomy specialists. It gives the possibility to design professional looking astronomy pictures in a few minutes.How To Create Presentation for Trainings and Learning process
Learning via presentations is used widely in education. This is a frequently used tool on trainings, especially for remote training via Skype.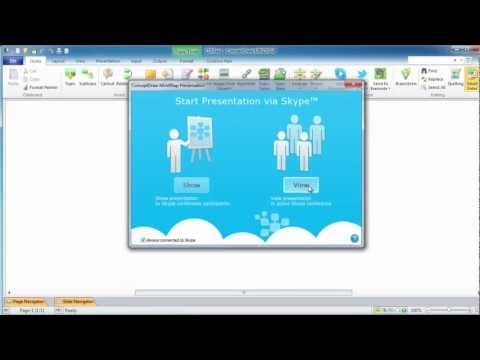
The vector stencils library "Zodiac constellations" contains 24 icons of Zodiac constellations star charts and Zodiac sign symbols.
Use these shapes to draw astronomical diagrams and illustrations in the ConceptDraw PRO diagramming and vector drawing software extended with the Astronomy solution from the Science and Education area in ConceptDraw Solution Park.
Use these shapes to draw astronomical diagrams and illustrations in the ConceptDraw PRO diagramming and vector drawing software extended with the Astronomy solution from the Science and Education area in ConceptDraw Solution Park.
TQM Diagram Tool
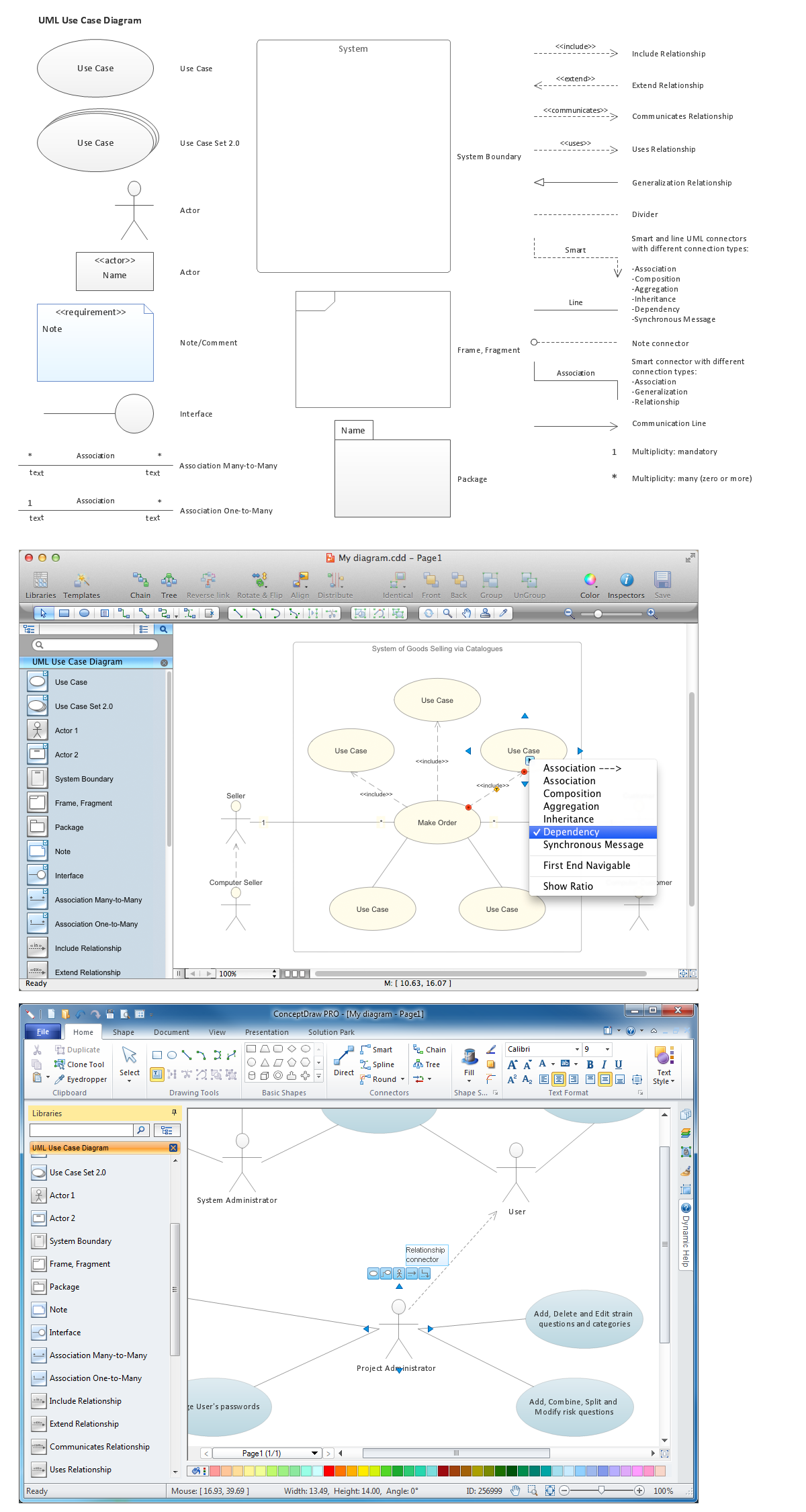
The Total Quality Management Diagram solution helps you and your organization visualize business and industrial processes. Create Total Quality Management diagrams for business process with ConceptDraw software.Diagramming Software for Design UML Use Case Diagrams
Use Case Diagrams describes the functionality provided by a system in terms of actors, their goals represented as use cases, and any dependencies among those use cases.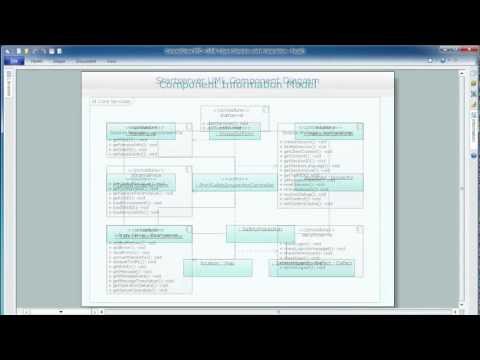
- Astronomy | How to Draw a Сonstellation Сhart | Design elements ...
- Solar System Symbols | Sun Solar System | Astronomy Symbols ...
- Astronomy Symbols | Astronomy and Astrology | Illustration Software ...
- Astronomy Symbols | Astronomy and Astrology | Solar System ...
- Astronomy Symbols | Sketching Software | Astronomy and Astrology ...
- Astronomy | Astronomy Symbols | Astronomy and Astrology ...
- Design elements - Astronomical symbols | Mathematics Symbols ...
- Astronomy and Astrology | Astronomy Symbols | Solar System ...
- Astronomy Symbols | Astronomy and Astrology | Astronomy Pictures ...
- Astronomy Pictures | Sun Solar System | Astronomy Symbols ...
- Sketching Software | Astronomy and Astrology | Astronomy Symbols ...
- Astronomy Symbols | Design elements - Astronomical symbols ...
- Beautiful Nature Scene: Drawing | Scientific Symbols Chart ...
- How to Draw a Сonstellation Сhart | Constellation Chart | Astronomy ...
- Astronomy and Astrology | Sun Solar System | Astronomy Symbols ...
- Astronomy Pictures | Astronomy Symbols | Astronomy and Astrology ...
- Zodiac constellations - Vector stencils library | Astronomy Symbols ...
- Astronomy Symbols | Summer triangle network | Diagrams Of Zodiac ...
- Saturn Drawing
- Electrical Symbols — Power Sources | Astronomy Symbols | Types ...